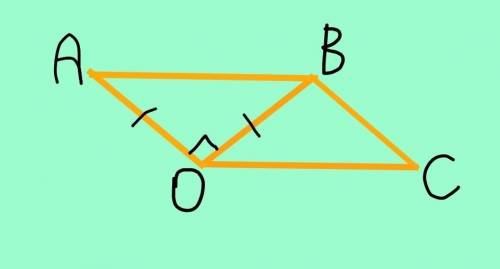
1 случай (с фото)
Пусть данная диагональ равна стороне, которой она перпендикулярна. Тоесть ВО=АО.
Тогда ∆АОВ равнобедренный с основанием АВ.
Углы при основании равнобедренного треугольника равны, тогда угол ОАВ=угол ОВА.
Исходя из этого: угол ОАВ+угол ОВА=2*угол ОАВ
Так как ВО перпендикулярно АО по условию, то угол ВОА=90°.
Следовательно ∆АОВ – прямоугольный с прямым углом АОВ.
Сумма острых углов в прямоугольном треугольнике равна 90°.
Составим уравнение:
Угол ОАВ+угол ОВА=90°
2*угол ОАВ=90°
Угол ОАВ=45°
Сумма углов при одной стороне параллелограмма равна 180°.
Следовательно: угол АОС=180°–угол ОАВ=180°–45°=135°
Противоположные углы параллелограмма равны.
Следовательно: угол ВСО=угол ОАВ=45°; угол СВА=угол АОС=135°
ответ: угол ВСО=угол ОАВ=45°; угол СВА=угол АОС=135°
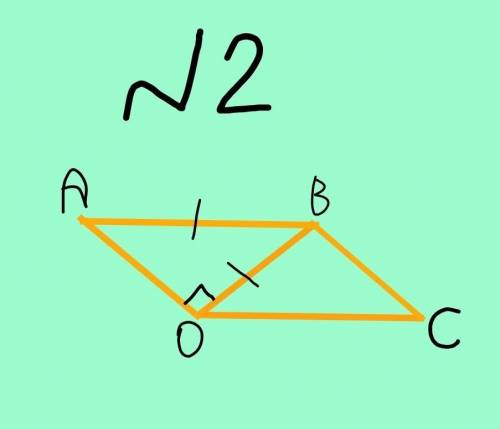
2 случай (с фото №2)
Пусть данная диагональ ВО равна НЕперпендикулярной ей стороне. Тоесть ВО=АВ.
Так как ВО перпендикулярно АО по условию, то угол ВОА=90°.
Следовательно ∆АОВ – прямоугольный с прямым углом АОВ.
Пусть АВ=х, тогда ВО=х так же.
По теореме Пифагора в прямоугольном ∆АОВ:
АВ²=АО²+ВО²
х²=АО²+х²
х²–х²=АО²
АО=√0
АО=0
Так как длина отрезка всегда положительная величина, то получим что ∆АОВ не существует.
А значит второго случая так же не существует.
Тогда ответ – ответ на 1 случай.
b11 = b1 * q^10 = 1/8
1/8 = (1/4) * q^10 / q^8
q^2 = (1/8) / (1/4) = 1/2
b1 = (1/4) / q^8 = (1/4) / (1/2)^4 = 2^4 / 2^2 = 2^2 = 4