Построив рисунок, получим прямоугольный треугольник с катетами 18 см и 24 см и гипотенузой-диаметром.
Находим диаметр по теореме Пифагора:
d²=18²+24²=324+576=900
d=30 cм
r=d/2=15 см
ответ. 15 см
S = 102 см²
Объяснение:
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам. Получается четыре прямоугольных треугольника, в которых гипотенузы равны стороне ромба, а катеты - половинам диагоналей. Тогда по Пифагору 26²= Х² +(Х-14)², где Х - половина большей диагонали. Из этого уравнения находим
Х = 7±√(49+240) = 17см.
Тогда половина меньшей диагонали равна 17-14 = 3см и площадь одного треугольника равна (1/2)*17*3 = 25,5см². Таких треугольников в ромбе четыре.
Площадь ромба равна 4*25,5 = 102см².
Можно через диагонали:
S=(1/2)*D*d = (1/2)*34*6 = 102 см².
Подробнее - на -
Відповідь:
Площа ромба 96 см2
Пояснення:
Периметр ромба це сума всіх його сторін, а оскільки всі сторони у ромба рівні, то сторона ромба = 10 см. Відома одна діагональ. Оскільки діагоналі ромба дііляться в точці перетину навпіл під прямим кутом, то утворюються 4 рівні прямокутні трикутники. Розглянемо трикутник з відомими двома сторонами 10 см та 12см : 2 = 6см. За теоремою Піфагора знайдемо половину другої діагоналі.
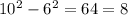
Половина другої діагоналі 8 см, то ж діагональ = 8*2=16 см
Тепер можемо знайти площу ромба за формулою:
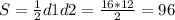
Вписанный угол, опирающийся на диаметр, прямой, поэтому
D = √ (18² + 24²) = √ 900 = 30 см, а R = 30 / 2 = 15 см.