Рассмотрим вариант, когда прямая имеет угловой коэффициент k>0, тогда она наклонена к положительному направлению оси ОХ под острым углом. Из чертежа видно, что угол наклона не может быть тупым, т.к. тогда S треугольника будет больше 3 .
От координатного угла отсекается ΔВОК , площадь которого S=3. Это прямоугольный треугольник, его площадь равна половине произведения катетов., то есть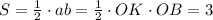 
.
Пусть ОК=3 ед. , а ОВ=2 ед. , тогда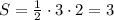 
.
Точка В в этом случае будет иметь координаты В(2,0), а точка К(0,-3) .
Подставим в уравнение прямой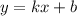 
координаты точки А(4,3) и , например, В(2,0), получим:
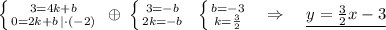
Или можно использовать то, что точка пересечения с осью ОУ имеет координаты К(0,-3). Тогда уравнение прямой имеет вид: y=kx-3 . И в это уравнение уже подставить координаты точки А(4,3) :
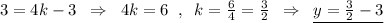
Также можно было составить уравнение прямой, проходящей через две точки А и В ( или А и К) .
Смотри рисунок.
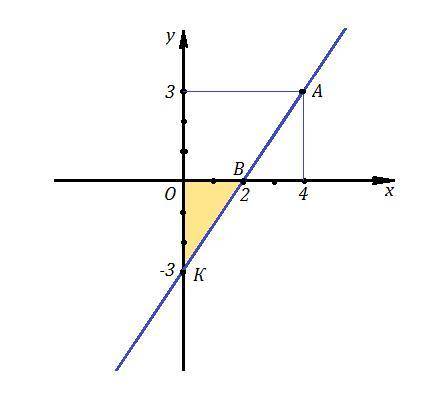
Рассмотрим вариант, когда прямая имеет угловой коэффициент k>0, тогда она наклонена к положительному направлению оси ОХ под острым углом. Из чертежа видно, что угол наклона не может быть тупым, т.к. тогда S треугольника будет больше 3 .
От координатного угла отсекается ΔВОК , площадь которого S=3. Это прямоугольный треугольник, его площадь равна половине произведения катетов., то есть .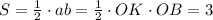
Пусть ОК=3 ед. , а ОВ=2 ед. , тогда .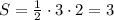
Точка В в этом случае будет иметь координаты В(2,0), а точка К(0,-3) .
Подставим в уравнение прямой 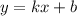координаты точки А(4,3) и , например, В(2,0), получим:
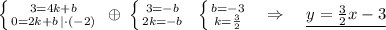
Или можно использовать то, что точка пересечения с осью ОУ имеет координаты К(0,-3). Тогда уравнение прямой имеет вид: y=kx-3 . И в это уравнение уже подставить координаты точки А(4,3) :
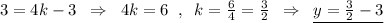
Также можно было составить уравнение прямой, проходящей через две точки А и В ( или А и К) .
Смотри рисунок.
высота пирамиды НО=12
Площадь основания So=6*8=48
Значит объем V=So*НО/3=48*12/3=192
В прямоугольнике диагонали равны и точкой пересечения делятся пополам
Значит диагональ АС=ВД=√6²+8²=√100=10
АО=ВО=СО=ДО=10/2=5
Из прямоугольного треугольника АНО найдем АН=√12²+5²=√169=13.
Значит АН=ВН=СН=ДН=13
Площадь треугольных граней можно найти по ф.Герона:
1) грани АВН и СДН: полупериметр р=(13+13+6)/2=16
Sавн=Sсдн=√16*(16-13)(16-13)(16-6)=12√10
2) грани ВСН и АДН: полупериметр р=(13+13+8)/2=17
Sвсн=Sадн=√17*(17-13)(17-13)(17-8)=12√17
Получается площадь бок. поверхности
Sбок=2Sавн+2Sвсн=2*12√10+2*12√17=24(√10+√17)
Sполн= Sбок+Sо=24(√10+√17)+48=24(√10+√17+2)