S = 45 см²
Объяснение:
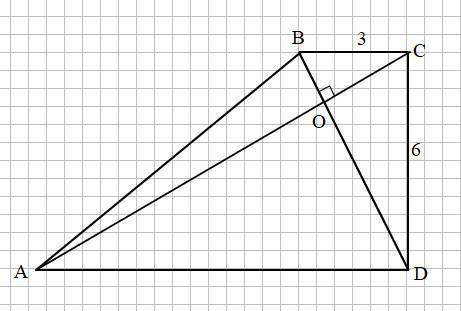
Смотри прикреплённый рисунок.
Найдём гипотенузу BD прямоугольного треугольника BCD.
По теореме Пифагора
BD² = ВС² + СD² = 3² + 6² = 45
BD = √45 = 3√5 (см)
Поскольку BD ⊥ AC, то СО является высотой, опущенной из вершины прямого угла С треугольника ВСD.
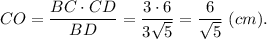
Известно, что высота, проведённая из вершины прямого угла данного прямоугольного треугольника делит этот треугольник на два треугольника подобных данному, поэтому ΔВОС ~ ΔCOD.
Коэффициент подобия k₁ = СD:BC = CO:BO = DO:CO
Из соотношения СD:BC = CO:BO найдём ВО
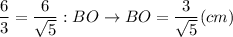
Из соотношения СD:BC = DO:CO найдём DO
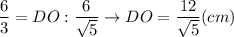
ΔВОС ~ ΔDOA по двум углам ( ∠СВО = ∠ADO - накрест лежащие при BC || AD и секущей BD: ∠BCO = ∠DAO - накрест лежащие углы при BC || AD и секущей АС)
k₂ = DO:BO = AD:BC
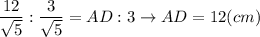
Площадь трапеции
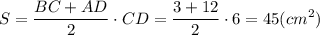
Sосн.=1/2 AC*CB
1)из △ACD: он прямоуг.Пусть CD=x,выражаем СА через tg30=CD/AC;=>AC=CD/tg30=x/1/√3=x√3
2)△DCB..таким же образом: СВ=CD/tg60=x/√3
3)△ABC:
Ac^2+CB^2=AB^2 по т.Пифагора,подставляешь:
(x√3)^2+(x/√3)^2=120;
3x^2+x^2=120|*3
9x^2+x^2=360;
10x^2=360;
x^2=36
x=+-6,это СД,далее самаи посчитайте,ответ 36