Завтра сдавать основание прямой призмы прямоугольного треугольника с гипотенузой 20 см и катетом 16 см.диагональ боковой грани,содержащей второй катет треугольника,равна 13 см.найти высоту призмы,боковую поверхность призмы,полную поверхность призмы

👇

Ответ:

fara32

22.11.2021

1)20^2-16^2=400-256=144(квадрат длины второго катета),тогда извлечем квадратный корень из144,получим второй катет в основании равен 12).
Рассмотрим боковую грань и найдем высоту,13^2-12^2=169-144=25,высота равна корень квадратный из 25=5.
2)боковая поверхность равна произведению периметра основания на высоту: (12+13+20)*5=45*5=225(см^2)
3)Полная поверхность равна сумме боковой поверхности и двух площадей оснований.Площадь основания равна половине произведения катетов:12*13/2=78
полная поверхность равна:225+2*78=225+156=381(см^2)

4,6(71 оценок)

Открыть все ответы

Ответ:

cozycoat1

22.11.2021

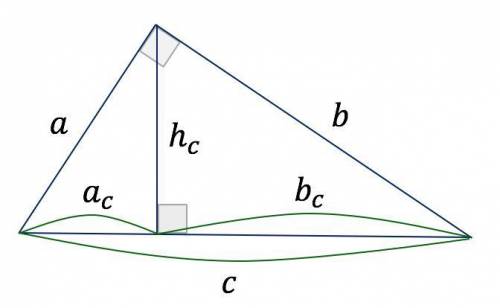
Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.

Перший б

Катет прямокутного трикутника — середнє пропорційне між гіпотенузою і проекцією цього катета на гіпотенузу:

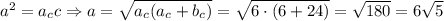$a^{2} = a_{c}c \Rightarrow a = \sqrt{a_{c}(a_{c}+ b_{c})} = \sqrt{6 \cdot (6 + 24)} = \sqrt{180} = 6\sqrt{5}$ см

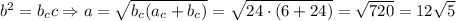$b^{2} = b_{c}c \Rightarrow a = \sqrt{b_{c}(a_{c}+ b_{c})} = \sqrt{24 \cdot (6 + 24)} = \sqrt{720} = 12\sqrt{5}$ см

Площа 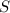прямокутного трикутника знаходится як півдобуток його катетів:

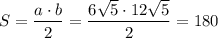$S = \dfrac{a \cdot b}{2} = \dfrac{6\sqrt{5} \cdot 12\sqrt{5}}{2} = 180$ см²

Другий б

Висота 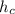$h_{c}$ прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:

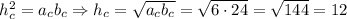$h^{2}_{c} = a_{c}b_{c} \Rightarrow h_{c} = \sqrt{a_{c}b_{c}} = \sqrt{6 \cdot 24} = \sqrt{144} = 12$ см

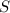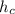Площа будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти $h_{c}$ , що до неї проведена:

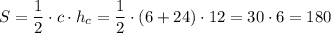$S = \dfrac{1}{2} \cdot c \cdot h_{c} = \dfrac{1}{2} \cdot (6 + 24) \cdot 12 = 30 \cdot 6 = 180$ см²

Відповідь: 180 см².

Знайдіть площу прямокутного трикутника , якщо висота проведена до гіпотенузи ,поділяє її на відрізки

4,6(95 оценок)

Ответ:

nurbibisaidova3

22.11.2021

>>> идёт оформление рисунка <<< ожидайте ...

Задача решается через векторы.
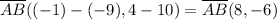Построим вектор $\overline{AB} ( (-1)-(-9) , 4-10 ) = \overline{AB} ( 8 , -6 )$ ;

Середина D отрезка AB может быть найдена откладыванием половины вектора $\overline{AB}$ от точки A

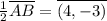$\frac{1}{2} \overline{AB} = \overline{ ( 4 , -3 ) }$ ;

Итак D( -9+4, 10-3 ) = D( -5, 7 ) ;

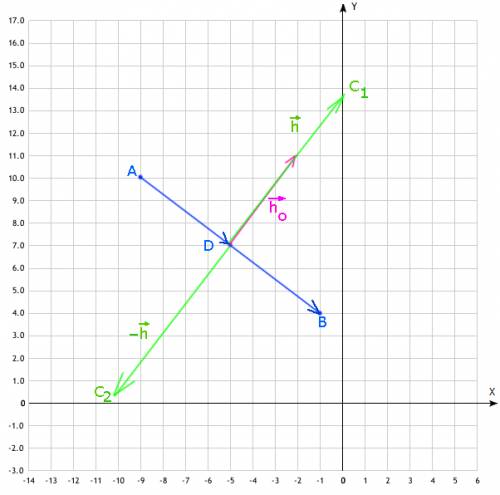
От точки D нужно отложить вектор высоты $\overline{h}$ в обе возможные стороны

Вектор высоты $\overline{h}$ перпендикулярен вектору основания $\overline{AB}$ , а значит его проекции накрест-пропорциональны с противоположным знаком:

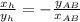(I) $\frac{x_h}{y_h} = -\frac{ y_{AB} }{ x_{AB} }$ , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться: $x_h * x_{AB} + y_h * x_{AB} = 0$ (II) ;

Таким образом вектор $\overline{h}$ пропорционален вектору $\overline{h_o} ( 3 , 4 )$ , поскольку для вектора $\overline{h_o}$ выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора $\overline{h}$ ;

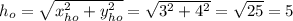Вектор $\overline{h_o}$ имеет длину $h_o = \sqrt{ x_{ho}^2 + y_{ho}^2 } = \sqrt{ 3^2 + 4^2 } = \sqrt{ 25 } = 5$ ;

Аналогично, AB = 10

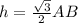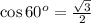При этом, поскольу треугольник равносторонний, то значит его высота составляет $h = \frac{ \sqrt{3} }{2}AB$ , т.к $\cos{ 60^o } = \frac{ \sqrt{3} }{2}$ ;

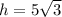Значит $h = 5 \sqrt{3}$ , а стало быть $h = \sqrt{3} h_o$ ;

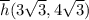В итоге $\overline{h} ( 3\sqrt{3} , 4\sqrt{3} )$ .

Откладываем этот вектор в разные стороны (+\-) от точки D( -5, 7 ) и получаем:

ОТВЕТ:

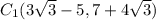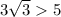$C_1 ( 3\sqrt{3} - 5 , 7 + 4\sqrt{3} )$ /// примечание: $3\sqrt{3} 5$ ;

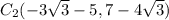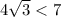$C_2 ( - 3\sqrt{3} -5 , 7 - 4\sqrt{3} )$ /// примечание: $4\sqrt{3} < 7$ .

Вычислить координаты вершины с равностороннего треугольника авс, если даны координаты а(-9,10), в(-1