Даны вершины треугольника A(1; 4); B(6; 5); C(4; -3).
Точка М = (B(6; 5) + C(4;-3)) / 2 = (4; 0,5).
Вектор АМ = М(4; 0,5) - A(-5; 1) = (9; -0,5).
Уравнение АМ: (x + 5) / 9 = (y - 1) / (-0,5) или в общем виде:
x + 18y - 13 = 0.
Высота BN перпендикулярна стороне АС.
Находим вектор АС = C(6; -3) - A(-5; 1) = (11; -4)
Уравнение АС: (x + 5) / 11 = (y - 1) / (-4) или в общем виде:
4x + 11y + 9 = 0.
Если к прямой Ax + By + C = 0 проведен перпендикуляр, то у него коэффициенты при переменных будут Bx - Ay.
Уравнение АС: 4x + 11y + 9 = 0.
Уравнение BN: 11x - 4y + C = 0. Для определения слагаемого С подставим координаты точки В, через которую проходит прямая BN.
11*2 - 4*4 + C = 0, отсюда С = 16 - 22 = -6.
Получаем уравнение BN: 11x - 4y - 6 = 0.
Находим угол:
Вектор АM Вектор ВN
х у х у
9 -0,5 11 -4
Модуль АM = 9,01387819 Модуль ВN = 11,7047
Угол между векторами
cos γ = 0,957303
γ = 0,293272 радиана
= 16,80328 градуса.
Объяснение:
Рисунок смотри на фото. Подробное объяснение здесь.
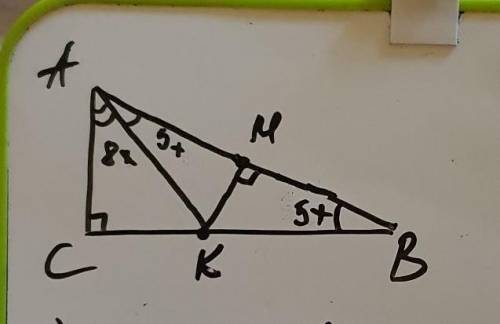
АМ=МВ (по условию, т.к. М середина гипотенузы)К - точка пересечения указанного перпендикуляра с катетом ВС∠САВ = 5х + 8х = 13х (т.к. КА делит ∠САВ в отношении 5:8 меньший угол при гипотенузе (по условию) => ∠САК = 8х, ∠МАК = 5х)△АКВ равнобедренный, т.к. △АМК=△ВМК по двум катетам и прямому углу => гипотенузы этих треугольников равны, т.е. АК=КВтогда ∠СВА = ∠КАВ = 5х (как углы при основании равнобедренного треугольника)△АСВ: ∠СВА + ∠САВ = 90°5х + 13х = 90
18х = 90 |÷18
х = 5
Следовательно:
▪︎∠СВА = 5 × 5 = 25°
▪︎∠САВ = 5 × 13 = 65°
проведем прямую МК параллельно АС, МР и КТ параллельно ВД
точки М, Р,Т,К лежат соответственно на ребрах пирамиды АВ, АД, СД,СВ
четырехугольник - прямоугольник, т.к.МР=ТК и МР||ТК и МР и ТК перпендикулярны плоскости АВС а значит и прямой МК
МК=2/3*а, т.к. треугольник АВС подобен треугольнику ВМК (прямая МК||АС отсекает треугольник подобный данному)и коэф подобия равен 2/3 (медианы пересекаются и точкой пересечения делятся в отношении 2:1 считая от вершины)
ВМ/ВА=ВК/ВС=2/3
треугольник ВДА подобен треуг МРА (ВД||МР)
АМ/АВ=1/3
МР=1/3*а
S(сечения)=2/3а*1/3а=2/9*а²
2)1)угол между плоскостями равен 60 градусов, т.к. угол АВС - линейный угол между плоскостями ВДА и ВДС
2)проведем ВН перпенд АС BH=√3/2*a
ДН перпендикулярна АС по теор о 3х перпендикулярах (ВД - перпендикуляр, ДН - наклонная, ВН - проекция наклонной)
угол ДНВ - линейный угол между плоскостями АВС и АСД
в прямоугольном треугольнике ВДН
tgDHB=DB/BH=a/(√3a/2)=2√3/3
DHB=arctg2√3/3
3)угол между прямой ВД и плоскостью ДАС - угол ВДН
tgВДН=√3а/2а=√3/2
ВДН=arctg√3/2