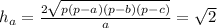
ответ:
якласс лого
1. теорема синусов, теорема косинусов
теория:
теорема синусов
теорему пифагора и тригонометрические функции острого угла можно использовать для вычисления элементов только в прямоугольном треугольнике.
для нахождения элементов в произвольном треугольнике используется теорема синусов или теорема косинусов.
4cepure.jpg
теорема синусов
стороны треугольника пропорциональны синусам противолежащих углов:
asina=bsinb=csinc
(в решении одновременно пишутся две части, они образуют пропорцию).
теорема синусов используется для вычисления:
неизвестных сторон треугольника, если даны два угла и одна сторона;
неизвестных углов треугольника, если даны две стороны и один прилежащий угол.
так как один из углов треугольника может быть тупым, значение синуса тупого угла находится по формуле sin(180°−α)=sinα .
наиболее часто используемые тупые углы:
sin120°=sin(180°−60°)=sin60°=3√2; sin150°=sin(180°−30°)=sin30°=12; sin135°=sin(180°−45°)=sin45°=2√2.
радиус описанной окружности
треуг2.jpg
asina=bsinb=csinc=2r , где r — радиус описанной окружности.
выразив радиус, получаем r=a2sina , или r=b2sinb , или r=c2sinc .
теорема косинусов
для вычисления элементов прямоугольного треугольника достаточно 2 данных величин (две стороны или сторона и угол).
для вычисления элементов произвольного треугольника необходимо хотя бы 3 данных величины.
4cepure.jpg
теорема косинусов
квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a2=b2+c2−2⋅b⋅c⋅cosa .
также теорема исполняется для любой стороны треугольника:
b2=a2+c2−2⋅a⋅c⋅cosb ;
c2=a2+b2−2⋅a⋅b⋅cosc .
теорема косинусов используется для вычисления:
неизвестной стороны треугольника, если даны две стороны и угол между ними;
вычисления косинуса неизвестного угла треугольника, если даны все стороны треугольника.
значение косинуса тупого угла находится по формуле cos(180°−α)=−cosα .
наиболее часто используемые тупые углы:
cos120°=cos(180°−60°)=−cos60°=−12; cos150°=cos(180°−30°)=−cos30°=−3√2; cos135°=cos(180°−45°)=−cos45°=−2√2.
если необходимо найти приблизительное значение синуса или косинуса другого угла или вычислить угол по найденному синусу или косинусу, то используется таблица или калькулятор.
вернуться в тему
следующее
copyright © 2019 якласс
контакты пользовательское соглашение
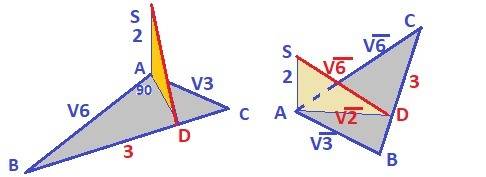
BD/AB = DC/AC
q/(2 + x) = 3/6
z/(y + 3) = 2/6
z= 8/5; q = 9/5
∠B = 90° (т.к. AB² + BC² = AC²)
ED = √(q² + z²) = (√145)/5