Відповідь:
3 см
Пояснення:
Відомо, що коло, вписане в трикутник, точками дотику до сторін відділяє рівні відрізки зі сторони кожної вершини.
Також відомо, що висоти - радіуси, проведені із центра такого кола в прямокутному трикутнику до катетів утворюють з відрізками від точок дотику до вершини прямого кута квадрат зі стороною, рівною радіусу вписаного кола.
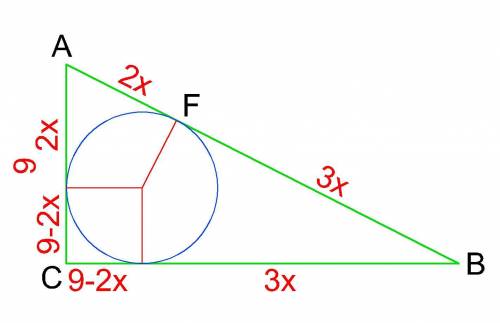
Згідно з умовою, позначимо AF як 2x, FB як 3x, тоді
r=9-2x
За теоремою Піфагора складемо рівняння:
9²+ (9-2х+3х)²=(2х+3х)²
81+(9+х)²=25х²
81+81+18х+х²-25х²=0
24х²-18х-162=0
4х²-3х-27=0
Дискрімінант: Д=9+4*4*27=441=21²
х₁=(3+21)/8=3 см
х₂=(3-21)/8=-2.25 см (не підходить).
Тоді r=9-2·3=3 см
1)Если периметр 12 см, то длина каждой стороны будет (12/4)=3 мм.
Тупой угол 120 гр. Тогда острый=60 градусов. Диагональ ромба делит угол пополам. Значит, получим 4 равных треугольника с острым углом 30 гр. А катет, лежащий против угла в 30 градусов, равен половине гипотенузы. Таким образом, катет будет (3/2)=1,5 мм. Второй катет по т.Пифагора можно найти.
Теперь легко вычислить площадь прямоугольного треугольника (S=1/2*a*b), а площадь ромба будет равна 4 площадям треугольника.
Дерзайте с вычислениями!
Трапеция АВСД : АД - большее основание, ВС - меньшее основание, АВ = СД - боковые стороны, АС -диагональ трапеции.
АС I СД; Обозначим АВ = СД = х; тогда АД = 3х/2., ВН = 10 - высота трапеции
Рассмотрим ΔАСД. Найдём в нём катет АС = √((3х/2)² - х²) = (х√5)/2
Площадь ΔАСД равна: с одной стороны, половине произведения катетов, т.е.
S = 0,5 АС·СД. А с другой стороны - половине произведения основания на высоту, т.е S = 0,5 AД·ВН. Приравняем правые части этих выражений
0,5 АС·СД = 0,5 АД·ВН
АС·СД = АД·ВН
(х√5)/2 · х = 3х/2 · 10
х²·√5 = 30х х ≠0
х√5 = 30
х = 30/√5 = 6√5
тогда большее основание равно АД = 3х/2 = 9√5
Рассмотрим ΔАВН и найдём катет АН по гипотенузе АВ = СД = х = 6√5 и катету ВН = 10, используя теорему Пифагора:
АН = √(АВ² - ВН²)= √(36·5 - 100) =√80 = 4√5
Меньшее основание трапеции ВС = АД - 2АН = 9√5 - 2·4√5 = √5
Площадь трапеции равна S = 0,5 (АД + ВС)·ВН = 0,5(9√5 + √5)·10 =
= 5·10√5 = 50√5
ответ: 50√5