МР = √41; МЕ = √34
Объяснение:
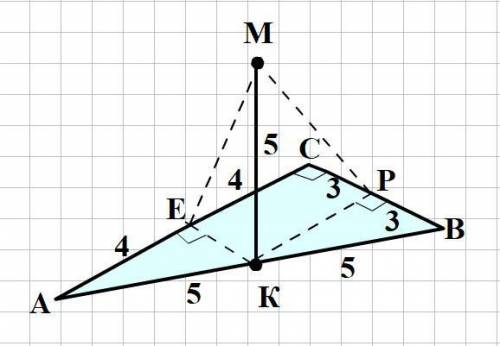
Смотри рисунок на прикреплённом фото.
Найдём гипотенузу АВ = √(АС² + ВС²) = √(8² + 6²) = 10
Из точки К проведём перпендикуляры КР и КЕ соответственно к сторонам ВС и АС. КР и КЕ являются средними линиями в ΔАВС.
КР = 0,5АС = 4; КЕ = 0,5ВС = 3.
Проведём наклонные МР и МЕ, которые и являются расстояниями от точки М до прямых ВС и АС, так как по теореме о 3-х перпендикулярах ВС ⊥ КР ⇒ ВС ⊥ МР и АС ⊥КЕ ⇒ АС ⊥МЕ.
Найдём МР и МЕ по теореме Пифагора.
МР = √(КР² + КМ²) = √(4² + 5²) = √41
МЕ = √(КЕ² + КМ²) = √(3² + 5²) = √34
в треугольнике АСМ углы МСА = МАС
угол СМВ будет внешним для треугольника АСМ, а внешний угол равен сумме внутренних углов треугольника, не смежных с ним
угол СМВ = 2*МСА
аналогично рассуждая про второй треугольник ВСМ, получим
угол СМА = 2*МСВ
углы СМВ и СМА смежные,
СМА + CМВ = 180°
2*МСВ + 2*МСА = 180°
МСВ + МСА = 90° = АСВ
1)
уголВ = х
уголА = х - 20
уголА = (180 - уголС) - 60
(180 - уголС) = уголА + уголВ
система
уголА = уголА + уголВ - 60
уголВ = 60°
уголА = 40°
уголС = (180 - 60 - 40) = 80°