6√1 см.
Объяснение:
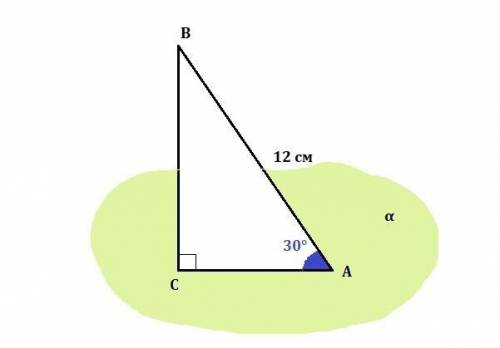
АВ - наклонная. АВ = 12 см
Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.Проведём из вершины В перпендикуляр ВС на плоскость α
ВС⊥α
Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости, и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной и той же точки, называется проекцией наклонной.АС - проекция наклонной АВ. ΔАВС - прямоугольный (∠С=90°)
Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.Угол ВАС - это угол между наклонной АВ и плоскостью α. ∠ВАС = 30° - по условию
Расстояние от точки до плоскости — равно длине перпендикуляра ВС, опущенного из точки на плоскость αВ прямоугольном треугольнике катет, лежащий против угла в 30° равен половине гипотенузы.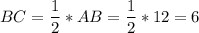
Расстояние от точки B до плоскости равно 6√1 см.
12
Объяснение:
Биссектриса АЕ (точка Е лежит на стороне ВС, не отмечено на рисунке).
ВС и АD - параллельные прямые, а прямая АЕ для них является секущей.
Отсюда следует, что угол ЕАD = углу АЕВ как накрест лежащие при параллельных прямых и секущей.
АЕ - биссектриса => угол ЕАD = углу ЕАВ.
В треугольнике АВЕ - два угла при одной стороне равны => он равнобедренный => сторона ВЕ = АВ.
АЕ делит сторону ВС в отношении 3:5, а значит ВЕ = 3х, ЕС = 5х.
Отсюда ВС = 3х+5х = 8х,
ВЕ = АВ = 3х,
АВ = СD по свойству параллелограмма = 3х,
АD = ВС по свойству параллелограмма = 8х.
Составляем уравнение:
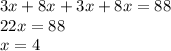
Меньшая сторона = 3х, а значит она равна 3*4=12
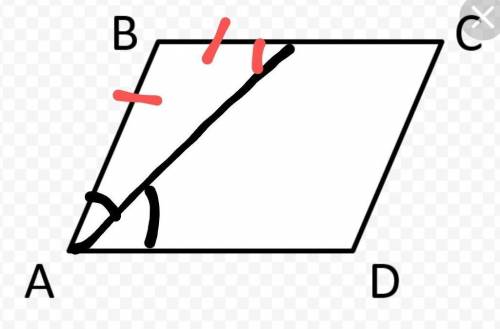
Рассмотрим треугольники АОВ и АОС:
АВ=АС (по условию)АО у них общая,
углы ОАВ и ОАС равны,так как равные наклонные
проведённые из одной точки к плоскости
следовательно треугольники равные
и значит ОВ=ОС
если посмотреть на треугольник ОВС:
ОВ=ВС
ОВ=ОС
ОВ=ОС=ВС
значит треугольник равносторонний и все углы равны
180:3=60 градусов