ответ: ∠ВАС = ∠ВСА = 30 ° ; ∠АВС = 120° .
Условия задачи:
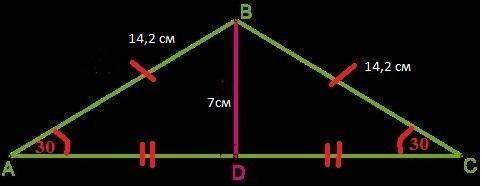
Δ АВС - равнобедренный , следовательно:
Боковые стороны равны ⇒ АВ=ВС = 14,2 см
Углы при основании равны :
АС - основание ⇒ ∠BAC (∠BAD) = ∠BCA (∠BCD)
BD =7,1 см - высота к основанию АС ⇒ является медианой и биссектрисой :
∠BDA = ∠BDC = 90° ( т.к. BD - высота)
AD = DC = АС/2 (т. к. BD - медиана)
∠ABD = ∠CBD (т. к. BD - биссектриса)
ΔBDA = ΔBDC - прямоугольные треугольники
Решение.
1) ΔBAD
По условию катет BD = 7,1 см , гипотенуза АВ = 14,2 см , следовательно :
BD = 1/2 * AB = 1/2 * 14,2 = 7,1 см
Если катет равен половине гипотенузы, то угол лежащий против этого катета равен 30° ⇒∠DAB (∠ BAC) = 30°
Проверим по определению синуса:
sin A = 7/14 = 1/2 ⇒ ∠BAC (∠BAD ) = ∠BCA (∠BCD) = 30°
2) ΔАВС :
Сумма углов любого треугольника = 180°
∠АВС = 180° - (∠ВАС + ∠ВСА)
∠АВС = 180 - 2*30 = 120 °
OK=ON=OE-это все радиусы вписанной окружности в трапецию
ОС -биссектриса <C, OD-биссектриса <D
<C+<D=180, значит <KCO+<KDO=90-как сумма половинок углов С и D
ΔCOD-прямоугольный так как <COD=180-( <KCO+<KDO)=90
ОК в нем высота, тогда
OK^2=CK*KD(теорема: высота в прямоугольном треугольнике из прямого угла-это средне геометрическое отрезков, на которые она делит гипотенузу)
OK^2=10*40=400
OK=20=ON
SK^2=OK^2+SO^2=400+125=525
SK=√525=5√21
OC^2=OK^2+CK^2=400+100=500
OC=10√5
SC^2=OC^2+SO^2=500+125=625
SC=25
1-Г
2-Д
3-А
4-Б
Угол C втрое больше, то есть C = 3 * A = 3 * 36 = 108 градусов.