1. Первоначальные сведения по геометрии появились за 4-5 тысячелетий до наших дней в Древнем Египте. В этих краях ежегодные разливы Нила смывали посевы. Поэтому для того чтобы восстанавливать посевы и уточнять размеры налогов, необходимо было размечать поля и выполнять необходимые подсчёты.
2. Древнегреческие учёные переняли у египтян измерения и учёта земель и назвали эти знания геометрией. "Геометрия" - слово, происходящее от греческих слов "reo" - земля, "метрео" - измерять.
3. Евклид, Пифагор, Мухаммад аль-Хорезми, Ахмад Фергани, Абу Райхан Беруни, Абу Али ибн Сина.
4. Памятник Кок Минор напоминает нам форму цилиндра, а на его поверхности фигуры, похожие на круги, овалы и ромбы.
5. Геометрия изучает пространственные структуры и отношения.
Объяснение:
Вроде всё!)
ответ: Объем шарового сегмента опущенного в цилиндр = π*468 см³
Объяснение: Дано:
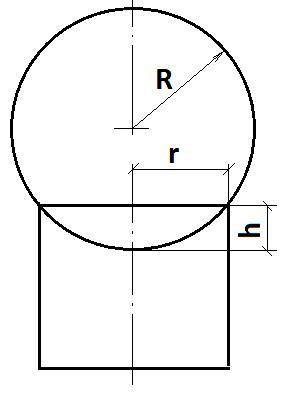
Диаметр шара = 30 см тогда его радиус R = 15
Радиус основания цилиндра r = 12см
Найти объем шарового сегмента, опушенного в цилиндр V - ?
Смотрите рисунок. Что бы найти объем надо найти размер h - глубину погружения шара. По теореме Пифагора R² = r² + (R-h)² Получили квадратное уравнение: h² - 2Rh + r² = 0
h1,2 = (2R+-√4R² - 4r²)/2 = (2R+-2√R²-r²)/2 h = 6 см
Объем шарового сегмента найдем по формуле V = π*h²(R - h/3) = π*468 см³
r = 3*ctg(π/6) = √3;
вообще треугольник CLM равносторонний, и хорда LM = 3 соответствует дуге 2π/3; в решении это не играет роли.
Далее, из теоремы косинусов для треугольника ABC
(x + 2)^2 = (x + 3)^2 + 5^2 - 2*5*(x + 3)*(1/2); где x = BK = BL;
Отсюда x = 5;
Ясно, что половина KL является высотой в прямоугольном треугольнике BKO с катетами OK = √3 и BK = 5;
BO = √(3 + 25) = 2√7;
KL = 2*OK*BK/BO = 2*√3*5/(2*√7) = 5√(3/7);