Пусть радиус самого большого полукруга R, тогда R = 126/2 = 63.
Пусть радиус среднего полукруга r₁, а радиус самого малого полукруга
r₂. Тогда r₂= 25.
r₁ = (126 - 2·25)/2 = (126 - 50)/2 = 76/2 = 38.
Пусть площадь большого полукруга S, среднего полукруга - S₁, малого полукруга S₂.
Тогда (по формуле площади круга, с учётом того, что у нас полукруги):
S = π·R²/2,
S₁ = π·r₁²/2,
S₂ = π·r₂²/2.
Тогда площадь заштрихованной области будет
= S - S₁ - S₂ = (π·R²/2) - (π·r₁²/2) - (π·r₂²/2) =
= π·( R² - r₁² - r₂²)/2 = π·( 63² - 38² - 25² )/2 = π·( 3969 - 1444 - 625)/2 =
= π·1900/2 = 950π.
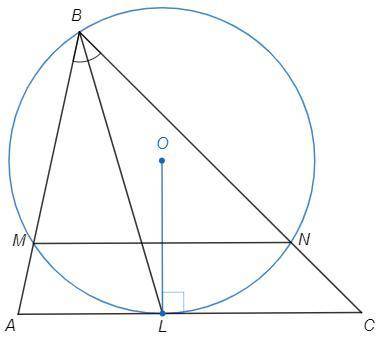
O - центр окружности
OL⊥AC (радиус в точку касания)
Биссектриса BL делит дугу MN пополам.
Радиус OL делит дугу MN пополам, следовательно перпендикулярен хорде MN.
(В равнобедренном △MON биссектриса OL является высотой.)
OL⊥AC, OL⊥MN => MN||AC
По теореме о биссектрисе
AB/AL =BC/CL
По условию
AB +BC =2AC =>
AL*AB/AL +CL*BC/CL =2AC =>
AB/AL (AL+CL) =2AC => AB/AL =2
По теореме о касательной и секущей
AL^2 =AB*AM => AL/AM =AB/AL =2
AL/AM *AB/AL =AB/AM =4/1
△MBN~△ABC (стороны параллельны) => MN/AC =MB/AB =3/4
по данному синусу вычислить косинус по основному тригонометрическому тождеству: (sinx)² + (cosx)² = 1
(cosx)² = 1 - 16/25 = 9/25
cosx = -3/5 для тупого угла
cosx = 3/5 для острого угла
c² = 16+100 - 2*4*10*(-3/5)
c² = 116 + 48 = 164
с = 2√41 ---сторона тупоугольного треугольника
c² = 16+100 - 2*4*10*(3/5)
c² = 116 - 48 = 68
с = 2√17 ---сторона остроугольного треугольника
решила оставить (вдруг все-таки опечатка)))
да))) не заметила сначала... если это не опечатка --- в единицах измерения сторон)))
4 метра и 10 см = 0.1 метра
c² = 16+0.01 - 2*4*0.1*(-3/5)
c² = 16.01 + 0.48 = 16.49
с = 0.1√1649 ≈ 4.06 м ---сторона тупоугольного треугольника
c² = 16+0.01 - 2*4*0.1*(3/5)
c² = 16.01 - 0.48 = 15.53
с = 0.1√1553 ≈ 3.94 м ---сторона остроугольного треугольника