меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
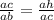
теперь подставим наши значения в эту пропорцию:
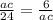
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

искомая проекция лежит в заданной плоскости проекции и эта плоскость принадлежит плоскости, которая проходит через заданную прямую перпендикулярно к заданной плоскости.
Чтобы вывести уравнение проецирующей плоскости, представим данную прямую в каноническом виде. найдем направляющий вектор прямой. найдя определитель разложив его по элементам первой строки.
→i →j →k
2 -1 1
1 1 2=
→i *(-2-1)- →j*(4-1)+ →k*(2+1)=→{-3-;3; 3}
найдем точку, которая лежит на прямой для этого положим z=0, решим систему
2х-у=3
-2х-2у=2, откуда у=-5/3, тогда х=-1-у=-1+5/3=2/3
Нашли точку, принадлежащую данной прямой (2/3; -5/3; 0)
т.е. прямая запишется в каноническом виде так
(х-2/3)/-3=(у+5/3)/-3=z/3
направляющий вектор заданной прямой →s={-3;-3;3}; нормальный вектор плоскости проекции {3; -1; 2/3) (у-5/31}. Тогда получим
находим определитель, разлагая его по элементам первой строки
(х-2/3) (у+5/3) z
-3 -3 3
3 1 1=
(х-2/3)*(-3+3)-(у+5/3)*(-6-9)+(z)*(3+9)=0
откуда 12у+20+12z=0, сократим на 4, получим 3х+3z+5=0, - уравнение проецирующей плоскости. а
искомая проекция задается системой уравнений, задающих плоскости проекции и проецирующую, т.е.
3у+3z+5=0
3x-y+z-4=0
ответ верный с)
3у+3z+5=0
3x-y+z-4=0
Косинус - наоборот (прилежащего к гипотенузе)
Тангенс - отношение противолежащего катета к прилежащему.
Котангенс - наоборот (прилежащего к противолежащему)