a) допустим, периметр = р, тогда сторона а=(p-6)
Так как Р=4а, то
Р=4*(p-6)
4p-24=p
4р-р=24
3p=24
p=24/4
p=8см
проверим 8-6=2см, Р=4*2=8см
б) допустим, дан ромб ABCD, точка O- пересечение диагоналей
диагональ=5см, половинна диагонали=2,5см
угол прилежащий к стороне =60, значит второй угол =30
Сторона лежащая против угла 30 градусов равна половине гипотенузы, то есть сторона ромба =2,5*2=5см
Р=4*а=4*5=20см
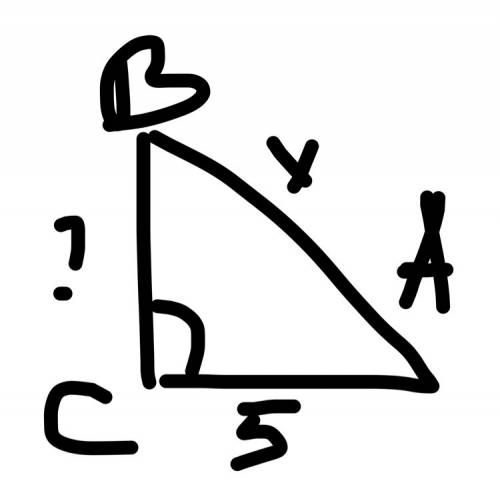
Составим уравнение по формуле x1/x2=y1/y2
n+5/5=-8/1-x
решим основываясь на свойстве пропорций a*d=b*c.
5*-8=-40 тоесть (x+5)*(1-x)=-40
(x+5)*(1-x)=-40
(-x+1)*(x+5)=-40
(-x+1)*(x+5)+40=0
(теперь вспомним правило умножения скобки на скобку)
(x*(-x+1)+5*(-x+1))+40=0
x*1=x
x*-x=-x^2
5*-x=-5x
5*1=5
в результате приходим к вот такому уравнению
упорядочиваем уравнение
x-5x=-4x
5+40=45
решаем получившиеся квадратное уравнение.
D = -4^2 - 4*-1*45 = 196
ответ: Векторы колинеарны при значениях n 5 и -9.
a) Пусть периметр равен р, тогда сторона равна (p-6)
Так как у ромба все стороны равны, то
4*(p-6)=p => 4p-24=p => 3p=24 =>p=24/4 =>p=8
б) Дан ромб ABCD, т. O- пересечение диагоналей
AC=5 => AO=OC=2,5
Угол BAO=60 => Угол ABO=30
Сторона лежащая против угла 30 градусов равна половине гипотенузы (сторона ромба), то есть AB=2,5*2=5
p=4*AB=4*5=20