41) ∠4 = 145°
43) ∠1 = 40
49) ∠AKD = 10°
Объяснение:
41) Поскольку ∠3 + ∠1 = 180 и ∠3 - ∠1 = 110 составим систему уравнений (пусть ∠3 = х, ∠1 = y ):
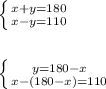
Решим вторую часть системы.
x - (180 - x) = 110
2x = 110 +180
2x = 290
x = 145
∠3 = 145°, следовательно ∠4 тоже будет равен 145°, так как это вертикальные углы.
43) ∠3 = 180° - ∠ACD(∠1+∠2) = 180 - 110 = 70° (так как смежные)
Поскольку CD - биссектриса ∠ECB, следовательно ∠3 = ∠2 = 70°
∠1 = 180 - ∠ECB (∠2+∠3) = 180 - 140 = 40° (опять-таки так как эти углы смежные)
49) Так как KE - биссектриса ∠CKB, тогда ∠EKB = ∠CKE = 40°
Так как DK ⊥CK, значит ∠ DKC = 90°
∠DKB = ∠EKB + ∠CKE + ∠DKC = 40 + 40 + 90 = 170°
∠AKD = 180° - ∠DKB = 180- 170 = 10° (так как ∠AKD и ∠DKB смежные)
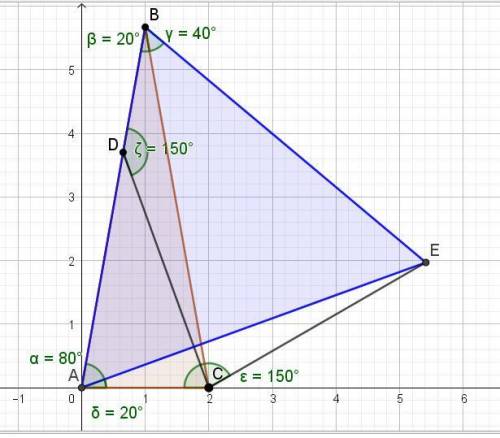
В треугольнике АВС углы при основании АС равны (180 - 20)/2 = 80°.
Построим равносторонний треугольник на стороне АВ.
Третью точку его Е соединим с точкой С.
Угол СВЕ = 60 - 20 = 40°.
Треугольник СВЕ равнобедренный, углы при его основании СЕ равны (180 - 40)/2 = 70°.
Тогда угол АСЕ = 80 + 70 = 150°.
Треугольник BCD равен треугольнику АСЕ по двум сторонам и углу между ними.
Угол CDB, равный 150 градусов - внешний треугольника ADC.
Тогда искомый угол ACD равен 150 - 80 = 70°.
ответ: угол ACD равен 70 градусов.
Во вложении дан пример решения аналогичной задачи.

h треугольника=2√3, вычисляется по формуле:
h=a√3/2 =>
a=2h/√3
a=2*(2√3)/√3
a=4
Sбок =Pосн* h
Sбок=3*4*2√3
Sбок=24√3