Алгоритм решения очень простой.
1. Точка М равноудалена от сторон, следовательно, её проекция на плоскость треугольника тоже будет равноудалена от сторон. Поэтому проекцией наклонной, являющейся кратчайшим расстоянием от М до любой из сторон, на плоскость треугольника, будет радиус вписанной в треугольник окружности r.
r = √(9^2 - 7^2) = 4√2;
2. Треугольник подобен треугольнику со сторонами 9 ,10, 11. Для треугольника со сторонами 9, 10 ,11 легко вычислить ПОЛУпериметр
р = (9 + 10 + 11)/2 = 15;
p - 9 = 6; p - 10 = 5; p - 11 = 4;
S^2 = 15*6*5*4; S = 30√2;
Для ЭТОГО треугольника (со сторонами 9, 10, 11) r = 30√2/15 = 2√2, а должен быть в 2 раза больше (см. первый пункт). Значит, и стороны должны быть в 2 раза больше.
Поэтому стороны треугольника равны 18, 20, 22.
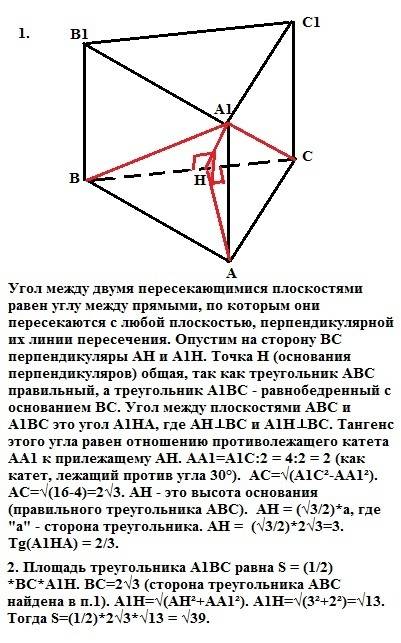
1. Определение: "Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения".
Опустим на сторону ВС перпендикуляры АН и А1Н. Точка Н (основания перпендикуляров) общая, так как треугольник АВС правильный, а треугольник А1ВС - равнобедренный с основанием ВС. Угол между плоскостями АВС и А1ВС это угол А1НА, где АН⊥ВС и А1Н⊥ВС. Тангенс этого угла равен отношению противолежащего катета АА1 к прилежащему АН. АА1 = А1С:2 = 4:2 = 2 (как катет, лежащий против угла 30°). АС=√(А1С²-АА1²). АС=√(16-4)=2√3. АН - это высота основания (правильного треугольника) АВС. АН = (√3/2)*а, где "а" - сторона треугольника. АН = (√3/2)*2√3=3.
Tg(A1HA) = 2/3.
2. Площадь треугольника А1ВС равна S = (1/2)*BC*A1H. ВС=2√3 (сторона треугольника АВС найдена в п.1). А1Н=√(АН²+АА1²). А1Н=√(3²+2²)=√13.
Тогда S=(1/2)*2√3*√13 = √39 ед².
3. В прямоугольном треугольнике АВС катет ВС лежит против угла 30° (дано) и равен ВС:2 = 2:2=1. Катет АС=√3. АА1В1В - квадрат, так как призма прямая, а <B1AB=45° (дано). Значит ВВ1=АВ=2.
В треугольнике АА1С: катет АА1=ВВ1=2, АС=√3. Тогда по Пифагору А1С=√(4+3)=√7. Треугольник А1СВ прямоугольный, так как А1С перпендикулярна ВС по теореме о трех перпендикулярах.
Площадь треугольника А1СВ равна S=(1/2)*A1C*BC = √7/2 ед².
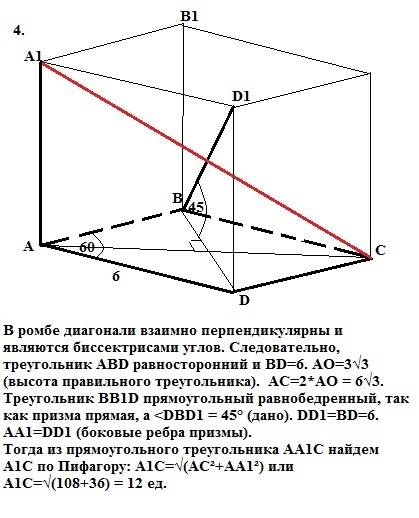
4. В ромбе диагонали взаимно перпендикулярны и являются биссектрисами углов. Следовательно, треугольник АВD равносторонний и BD=6см. АО=3√3см (высота правильного треугольника). АС=2*АО = 6√3см. Треугольник BB1D прямоугольный равнобедренный, так как призма прямая, а <DBD1 = 45° (дано). DD1=BD=6см. АА1=DD1 (боковые ребра призмы). Тогда из прямоугольного треугольника АА1С найдем А1С по Пифагору: А1С=√(АС²+АА1²) или
А1С=√(108+36) = 12 см.