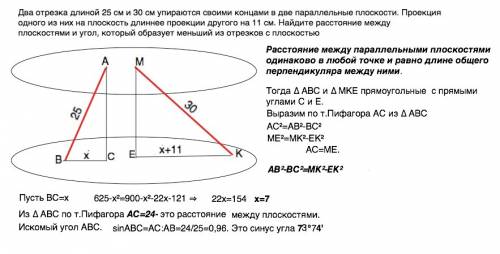
Пусть отрезки будут АВ=25 см с проекцией ВС и МК=30 см с проекцией КЕ.
Расстояние между параллельными плоскостями одинаково в любой точке и равно длине общего перпендикуляра между ними.
Тогда ∆ АВС и ∆ МКЕ прямоугольные с прямыми углами С и Е.
Выразим по т.Пифагора АС из ∆ АВС
АС²=АВ²-ВС²
МЕ²=МК²-ЕК²
АС=МЕ.
АВ²-ВС²=МК²-ЕК²
Пусть ВС=х
625-х²=900-х²-22х-121 ⇒
-900+625+121= х²-х²-22х Проведя необходимые вычисления, получим
22х=154 ⇒ х=7
Из ∆ АВС по т.Пифагора АС=24- это расстояние между плоскостями.
Искомый угол АВС.
sin∠ABC=АС:АВ=24/25=0,96. Это синус угла 73°74'
Доказательство: (см. рис.)
Пусть параллельные прямые а и b пересечены секущей АВ.
Тогда соответственные ∠1 и ∠2 будут равны,
∠2 и ∠3 – смежные, поэтому ∠2 + ∠3 = 180°.
Из равенств ∠1 = ∠2 и ∠2 + ∠3 = 180° следует, что
сумма односторонних углов ∠1 + ∠3 = 180°.
Теорема доказана.