∠ACB = 65°
Объяснение:
Дано:
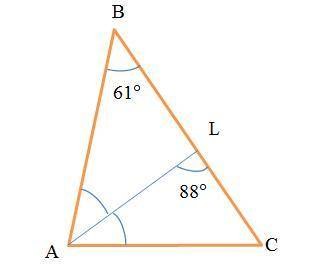
В ΔABC (см. рисунок)
∠ABC=∠ABL=61°
∠ALC=88°
Найти: ∠ACB
Решение.
Так как ∠ALC=88°, то смежный с ним угол ∠ALB=180° - 88° = 92°.
Используем свойство: сумма внутренних углов треугольника равна 180°: ∠АLB+∠АBL+∠BАL=180°
Отсюда:
∠BAL = 180° - ∠ALB - ∠АBL = 180° - 92° - 61° = 27°.
Биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠BAL = 2·27° = 54°.
Ещё раз используем свойство: сумма внутренних углов треугольника равна 180°: ∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 54° - 61° = 65°.
ответ: ∠ACB = 65°.
если в треугольнике АВС проведена высота СD и АС= 12, ВС= 5, то по т. Пифагора x^2= 144+25, x= 13, значит АВ= 13. Значит АС= корень (АВ*АD), АС^2= АD*АВ, 144= 13AD, АD= 144/13
АВ= АD+ DВ, из этого следует, что DB=13-144/13, DB= 25/13
Высота прямоугольного треугольника к гипотенузе, есть среднее пропорциональное отрезков, на которые делится эта гипотенуза:
CD= корень (АD*DB), CD= корень (144/13*25/13), СD= корень (3600/169), CD= 60/13