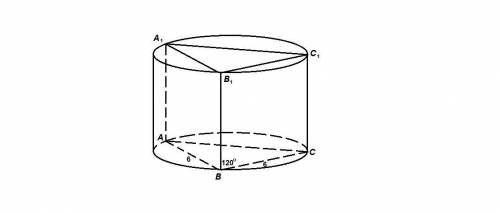
Прямая призма АВСА₁В₁С₁ вписана в цилиндр. АВ = ВС = 6, ∠АВС = 120°, АА₁ = 10.
Найти площадь боковой поверхности цилиндра.
ответ: 120π
Объяснение:
Если прямая призма вписана в цилиндр, то высота цилиндра равна длине бокового ребра призмы:
Н = АА₁ = 10,
а основания цилиндра описаны около оснований призмы.
ΔАВС равнобедренный, тогда
∠А = ∠С = (180° - 120°)/2 = 30°
Радиус окружности, описанной около треугольника, можно найти по формуле:
R = AB / (2 sin∠C) = 6 / (2 · 1/2) = 6
Площадь боковой поверхности цилиндра:
Sбок.цил. = 2πR · H = 2π · 6 · 10 = 120π кв. ед.
AB ==> ?
<A = 45°⇒ <B=90°-<A=90°- 45° = 45°⇔ CA =CB ( ΔCAB_равнобедренный), поэтому
AH =BH ( высота одновременно и медиана ) .
AB =2AH , но AH = CH (ΔAHC тоже равнобедренный) , действительно
<A = 45°⇒<ACH =90° - <A = 90°- 45°=45° =<A .
AB =2CH= 2*8 см =16 см
ответ : 16 см .