Возьмём стороны за х. Тоесть одна сторона 4х а вторая 3х, Диагональ равна 20 и является гиппотенузой прямоугольного треугольника(в котором один катет-4х, а второй3х). По теорме Пифагора составим уровнение
Получаем
Складываем 25^2=400
ответ
отсюда х=4, а так как одна сторона = 4х, а вторая 3х, то большая сторона = 4*х(4)
Примем длины рёбер за 1. Ромб с острым углом 60 градусов имеет меньшую диагональ, равную стороне. Половина такого ромба - равносторонний треугольник. Опустим из точек В и Д перпендикуляры на боковое ребро. Они пересекутся в точке К. Треугольник ВКД - равнобедренный. В основании - диагональ ВД = 1. КВ = КД = 1*cos 30° = √3/2. Искомый угол ВКД равен : ∠BKD = 2arcsin((1/2)/(√3/2) = 2arcsin( 1/√3) = 2arcsin(√3/3) = 70,52878°.
NM║CB ⇒ ∠SNM = ∠SCB; ∠SMN = ∠SBC как соответственные углы ⇒ ΔSCB ~ ΔSNM по двум равным углам ⇒ ⇒ Т.к. фигура в сечении пирамиды плоскостью, параллельной основанию, подобна основанию, то ΔABC ~ ΔKMN с коэффициентом подобия k = Площади подобных фигур относятся как коэффициент подобия в квадрате
Возьмём стороны за х. Тоесть одна сторона 4х а вторая 3х, Диагональ равна 20 и является гиппотенузой прямоугольного треугольника(в котором один катет-4х, а второй3х). По теорме Пифагора составим уровнение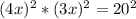
Получаем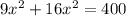
Складываем 25^2=400
ответ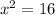
отсюда х=4, а так как одна сторона = 4х, а вторая 3х, то большая сторона = 4*х(4)
ответ: большая сторона 16