1) Сумма углов треугольника 180°
В ∆ АВС ∠ АВС+∠ВАС=180°- 40°=140°
Сумма развернутых углов ∠НВС+∠КАС=360°
∠НВА+∠КАВ=360°- (∠ АВС+∠ВАС)=360°-140°=220°
Биссектрисы углов НВМ и КАВ делят их пополам.
Сумма половин этих углов вдвое меньше.
∠DBA+∠DAB=220:2=110°
∠BDA=180°-110°=70°
2)
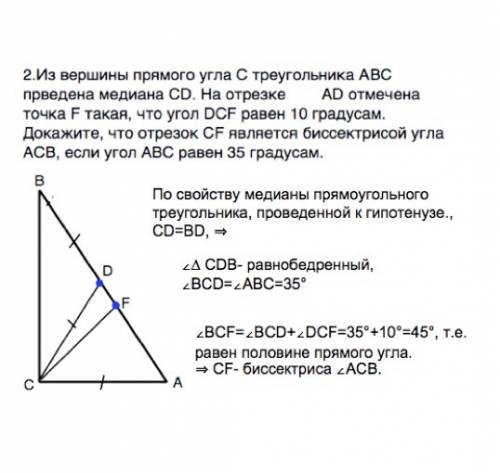
По свойству медианы прямоугольного треугольника, проведенной к гипотенузе., CD=BD, ⇒
∠∆ CDB- равнобедренный, ∠ВСD=∠ABC=35°
∠ВСF=∠BCD+∠DCF=35°+10°=45°, т.е. равен половине прямого угла.
⇒ CF- биссектриса ∠АСВ.
3)
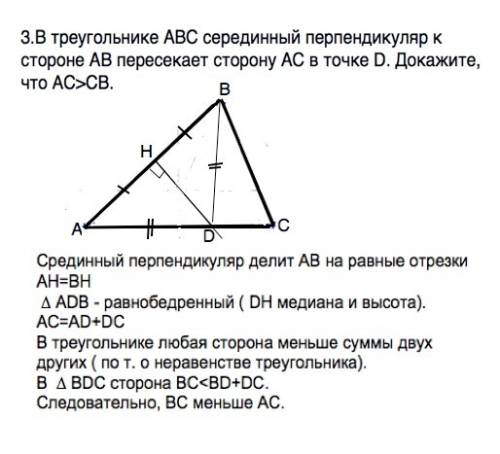
Срединный перпендикуляр делит АВ на равные отрезки АН=ВН
∆ АDВ - равнобедренный ( DH медиана и высота).
АС=AD+DC
В треугольнике любая сторона меньше суммы двух других ( по т. о неравенстве треугольника).
В ∆ ВDС сторона ВС < ВD+DC, а BD=AD. ⇒ ВС < AD+DC
Следовательно, ВС меньше АС.

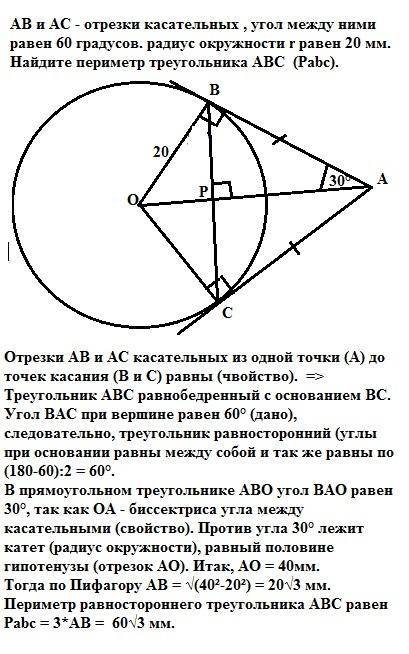
Отрезки АВ и АС касательных из одной точки (А) до точек касания (В и С) равны (свойство). =>
Треугольник АВС равнобедренный с основанием ВС.
Угол ВАС при вершине равен 60° (дано), следовательно, треугольник равносторонний (углы при основании равны между собой и так же равны по (180-60):2 = 60°.
В прямоугольном треугольнике АВО угол ВАО равен 30°, так как ОА - биссектриса угла между касательными к окружности (свойство). Против угла 30° лежит катет (радиус окружности), равный половине гипотенузы (отрезок АО). Итак, АО = 40мм.
Тогда в треугольнике АОВ по Пифагору АВ = √(40²-20²) = 20√3 мм.
Периметр равностороннего треугольника АВС равен
Pabc = 3*АВ = 60√3 мм.
угол В=90º.
1) угол ВАС 60º(по условию), тогда угол АСВ равен 30º т.к. сумма всех углов треугольника 180º
2) по свойству прямоугольного треугольника, катет, лежащий против угла в 30º градусов равен половине гипотенузы. Следовательнл АС=2×АВ=2×8=16см.
По теореме пифагора АС^2=АВ^2+ВС^2
16^2=8^2+ВС^2
256=64+ВС^2
ВС^2=192
ВС= корень из 192.
S=AB×BC
S=8×корень из 192.
ответ:8×8корень из 3 =64×корень из 3 ( такой ответ так как сократили)