Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI
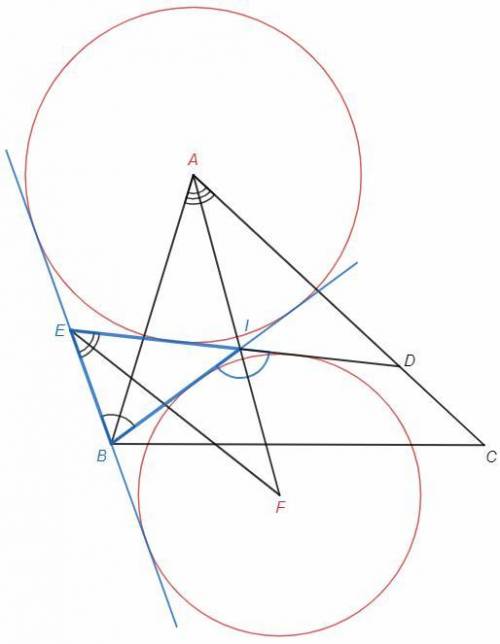
Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI

Решить треугольник, значит найти все его элементы.
В условии точно дано AB=6? Или может написано а=6? Потому что, если АВ, то придется вычислять некоторые значения приблизительно(такие как sin105), а если а=6, то значения будут точные проверить условие, если действительно ошиблись, то напишите в личку, подправлю решение.
Сначала, найдем третий угол.
<C=180-<A-<B по теореме о сумме углов треугогльника
<C=180-30-45=105
Теперь, используя теорему синусов найдем сторону CB:
CB/sin30 = AB/sin105
CB=ABsin30/sin105=6*0,5/0,966=3,1 см
По теореме синусов найдем сторону AC:
AC/sin45=AB/sin105
AC=ABsin45/sin105=[tex]6*\frac{\sqrt{2}}{2}/0,966=4,4