1. По двум сторонам и углу между ними (АО=ОВ; угол АОС = углу СОБ, а ОС - общая сторона).
1.2) По стороне и прилежащим к ней углам (ВДА = АДС; АД - общая сторона; БАД = ДАС)
2. Сначала нужно доказать равенстао треугольников (по стороне и прилежащим к ней. углам; углы СОА = БОД (вертикальные); углы А= Б по условию.
2.2) Теорема Фалеса. По двум сторонам и углу между ними (АО=ОВ; угол АОС = углу СОБ, а ОС - общая сторона).
1.2) По стороне и прилежащим к ней углам (ВДА = АДС; АД - общая сторона; БАД = ДАС)
2. Сначала нужно доказать равенстао треугольников (по стороне и прилежащим к ней. углам; углы СОА = БОД (вертикальные); углы А= Б по условию.
2.2) Теорема Фалеса. Параллельные прямые отсекают на секущих пропорциональные отрезки
S1 ≈ 19,8 cм².
S2 ≈ 3,9 cм².
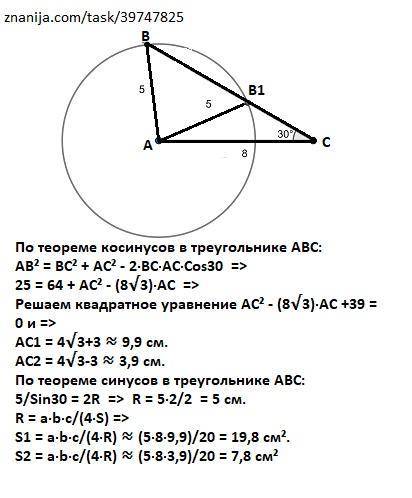
Объяснение:
По теореме косинусов в треугольнике АВС:
АВ² = ВС² + АС² - 2·ВС·АС·Сos30 =>
25 = 64 + AC² - (8√3)·AC =>
Решаем квадратное уравнение AC² - (8√3)·AC +39 = 0 и =>
AC1 = 4√3+3 ≈ 9,9 см.
АС2 = 4√3-3 ≈ 3,9 см.
По теореме синусов в треугольнике АВС:
5/Sin30 = 2R => R = 5·2/2 = 5 см.
R = a·b·c/(4·S) =>
S1 = a·b·c/(4·R) ≈ (5·8·9,9)/20 = 19,8 cм².
S2 = a·b·c/(4·R) ≈ (5·8·3,9)/20 = 7,8 cм²
P.S. Для проверки на рисунке выполнено точное построение, доказывающее, что задача имеет два решения.
TS | | AB ⇒ MN | | TS и MN = TS ( т.к. они равны половине АВ)
А это признак того, что MNTS - параллелограмм ⇒ M,N,T,S лежат в одной плоскости.