Площадь боковой поверхности равна 756 дм².
Площадь полной поверхности равна 1145 дм².
Объяснение:
Площадь боковой стороны усеченной пирамиды равна площади равнобочной трапеции с основаниями 17 и 10 дм и высотой, равной апофеме 14 дм.
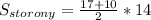
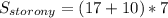
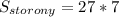
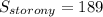 дм².
дм².
В площади боковой стороны таких трапеций четыре.
Значит
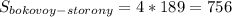 дм².
дм².
Площадь полной поверхности равна сумме площади боковой поверхности и площадей оснований.
Площадь меньшего основания равна площади квадрата со стороной 10 дм
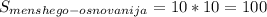 дм².
дм².
Площадь большего основания равна площади квадрата со стороной 17 дм
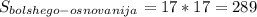 дм².
дм².
Теперь надо сложить все эти три площади
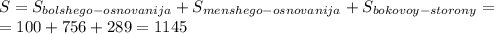
дм².
В равнобедренном треугольнике две боковые стороны равны.
Если заданы две стороны равнобедренного треугольника 12 и 6, и нет пояснения, какая из сторон боковая, а какая сторона - основание, то возможны 2 варианта .
Если неизвестная сторона -боковая, то она может быть равна 6 . Тогда в треугольнике стороны равны 6, 6, 12 .
Но для таких длин сторон треугольника не выполняется неравенство треугольника: сумма двух сторон треугольника больше длины третьей стороны; 6+6=12, но (6+6) не больше 12. Не существует треугольника со сторонами 6, 6, 12.
Если неизвестная сторона -боковая, то она может быть равна 12 . Тогда в треугольнике стороны равны 12, 12, 6 .
Неравенство треугольника выполняется: 12+12>6 , 12+6>12.
Аналогично, если неизвестная сторона - основание, то оно может быть равна или 6, или 12. Тогда две боковые стороны равны в первом случае по 12, а во втором случае по 6 . То есть опять получаем два треугольника, один со сторонами 6, 12, 12 , а второй со сторонами 12, 6, 6 , который не существует .
ответ: сторона равнобедренного треугольника может быть равна 12 .
CHB - прямоугольный, по теореме Пифагора найдем CH=
CO:OH=2:1 (по свойству медианы)
OC=
SOC- прямоугольный, тогда по теореме Пифагора найдем высоту
SO=