Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
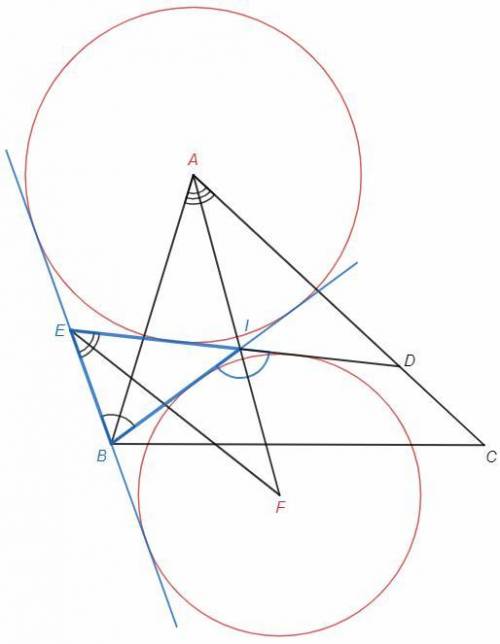
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI
Площадь боковой поверхности цилиндра равна площади прямоугольника, длина которого равна длине окружности основания цилиндра, а ширина - образующей ( высоте) цилиндра.
S бок=2 πrН
Обозначим хорду АВ, центр верхнего основания цилиндра С, центр нижнего основания - О.
Расстояние от точки до прямой измеряется перпендикулярным к ней отрезком.
Соединим А и В с центрами окружностей. В треугольники АВС отрезок СН - его высота и по условию равна 13.
ОН - расстояние от центра нижнего основания до хорды и перпендикулярно ей. СО - высота цилиндра и перпендикулярно основаниям.
Треугольник СОН - прямоугольный, из троек Пифагора, и поэтому можно, не считая, узнать длину катета СО=12 см ( проверьте).
Треугольник СОВ - прямоугольный ( СО - перпендикуляр).
Гипотенуза ВС =15 см, СО=12 см, треугольник «египетский»,
ВО=9 см ( проверить можно по т.Пифагора),
Высота ( как и образующая) цилиндра равна 12 см,
радиус ВО=9 см
S бок=2 π*9*12=216 π см²