Расстояние от точки до прямой измеряется длиной отрезка, проведенного перпендикулярно этой прямой.
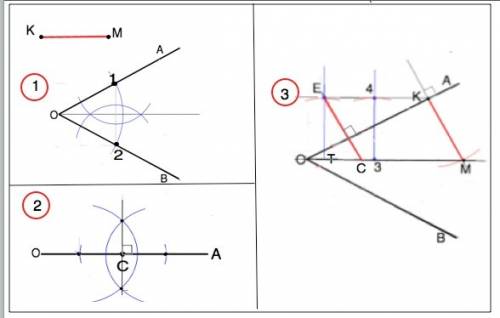
Обозначим угол АОВ, заданный отрезок – КМ. Любая точка, лежащая на биссектрисе угла, равноудалена от сторон этого угла.(свойство биссектрисы)
Следовательно, точка, равноудаленная от сторон угла АОВ, лежит на его биссектрисе.
1. Построение биссектрисы (рис.1 приложения).
Из т. О как из центра произвольным раствором циркуля отметим на сторонах угла точки 1 и 2. Из этих точек раствором циркуля взятым так, чтобы он был больше половины расстояния между точками 1 и 2, проведем полуокружности до их пересечения двух точках. Точки пересечения и вершину угла соединим. Биссектриса построена.
2. Из произвольной точки С на биссектрисе проведем к стороне ОА перпендикуляр и отметим на нем отрезок СЕ, равный заданному отрезку КМ. ( как это делать - Вы наверняка знаете. см. рис. 2)
3. Из т.Е проведем прямую параллельно биссектрисе.
Для этого из т. Е опустим на прямую, содержащую биссектрису, перпендикуляр ЕТ. Из произвольной точки 3 возведем второй перпендикуляр и отложим на нем отрезок, равный отрезку ТЕ в т.4. Проведем через Е и т.4 прямую до пересечения со стороной угла АОВ в т.К.
4. Из т.К проведем перпендикуляр к стороне ОА. Он пересечется с биссектрисой в т.М, параллелен ЕС, его длина равна длине заданного отрезка (свойство параллельных прямых, пересекающих другие параллельные прямые). .
Точка М - искомая, расстояние от нее до другой стороны угла по свойству биссектрисы равно КМ.
p=(a+b+c)/2=(9+10+17)/2=18;
S=корень (p*(p-a)*(p-b)*(p-c))=корень (18*9*8*1)=36;
Площадь параллелограмма в основании 2S=72.
2) Пусть высота прямого параллелепипеда равна h. Боковые грани прямого параллелепипеда - это прямоугольники. Тогда площадь 4 прямоугольников боковой поверхности 2*(9h+10h)=38h, а площадь полной поверхности 38h+2*72=38h+144. Сказано, что площадь полной поверхности равна 334:
38h+144=334;
38h=190;
h=5.
3) Объём прямого параллелепипеда равен произведению площади основания на высоту:
V=72*h=72*5=360.
ответ: 360.