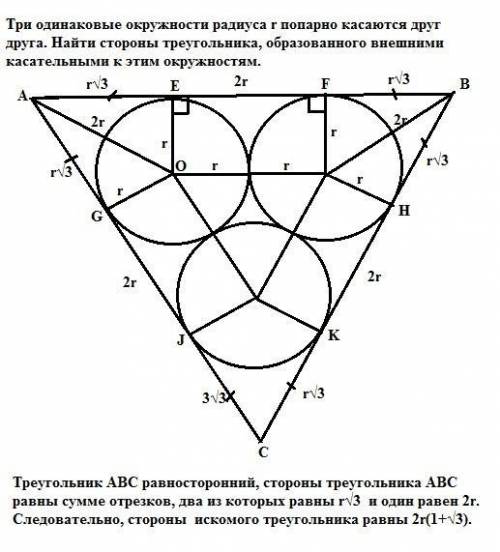
Стороны искомого треугольника равны 2r(1+√3).
Объяснение:
АВ, АС и ВС - касательные к попарно касающимся окружностям радиуса r.
Отрезки AE=AG, CJ=CK, BF=BH как отрезки касательных, проведенных к окружности из одной точки. Отрезки EF=GJ=KH= 2r как противоположные стороны прямоугольников, образованных радиусами окружностей, проведенных в точки касания и отрезками, соединяющими центры касающихся окружностей, равными сумме радиусов этих окружностей. Таким образом, треугольник АВС равносторонний, так как его стороны равны сумме равных отрезков.
Углы равностороннего треугольника равны 60°.
Рассмотрим треугольник АОЕ. Угол ЕАО = 30° (так как АО - биссектриса по свойству отрезка, соединяющего общую точку касательных к окружности с центром этой окружности). Катет против угла 30° равен половине гипотенузы => AO=2r => AE = r√3.
Итак, стороны треугольника АВС равны сумме отрезков, два из которых равны r√3 и один равен 2r. Следовательно, стороны искомого треугольника равны 2r(1+√3).
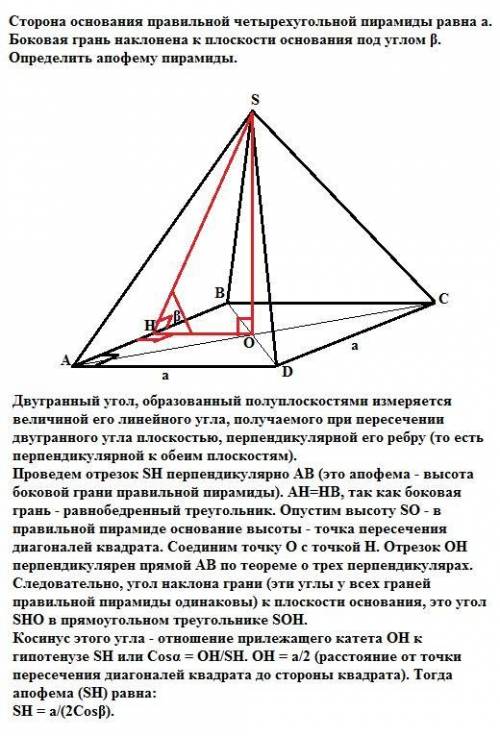
SH = a/(2Cosβ).
Объяснение:
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Проведем отрезок SH перпендикулярно АВ (это апофема - высота боковой грани правильной пирамиды). АН=НВ, так как боковая грань - равнобедренный треугольник. Опустим высоту SO - в правильной пирамиде основание высоты - точка пересечения диагоналей квадрата. Соединим точку О с точкой Н. Отрезок ОН перпендикулярен прямой АВ по теореме о трех перпендикулярах.
Следовательно, угол наклона грани (эти углы у всех граней правильной пирамиды одинаковы) к плоскости основания, это угол SHO в прямоугольном треугольнике SOH.
Косинус этого угла - отношение прилежащего катета ОН к гипотенузе SH или Cosα = OH/SH. OH = a/2 (расстояние от точки пересечения диагоналей квадрата до стороны квадрата). Тогда апофема (SH) равна:
SH = a/(2Cosβ).
:)