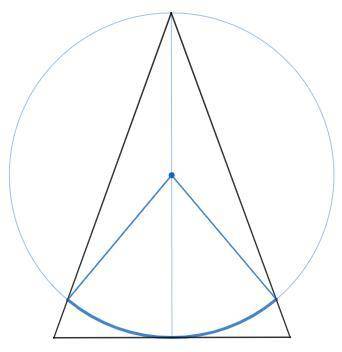
Угол при основании равнобедренного треугольника равен 70°. На высоте треугольника, проведенной к основанию и равной 27 см, как на диаметре построена окружность. Найдите длину дуги окружности, которая принадлежит треугольнику.
Длина окружности диаметром d равна пd
Длина дуги ф градусов равна пd *ф/360°
Диаметр известен, 27 см.
Найдем угол между радиусами.
Он вдвое больше угла против основания.
(Вписанный угол равен половине центрального, опирающегося на ту же дугу.)
Угол против основания 180-70*2=40
Угол искомой дуги 40*2=80
L =27п *80°/360° =6п (см)
Значит внутренний,смежный с ним угол равен
180-125=55 градусов
А два внутренних не смежных с внешним угла равны в сумме
125 градуса
Треугольник равнобедренный,значит два угла при основании равны между собой,т е один угол 55 градусов и второй 55 градусов,а основание равно
180-110=70 градусов
Опять же-заказчик решения не предоставил чертёж
Вариант второй
Можем предположить,что 55 градусов равен угол при вершине,а углы при основании в сумме равны 125 градусов,т к они равны между собой, то каждый из них равен
125:2=62,5 градусов
Объяснение:
BC=√(-2-4)²+(6-0)²+(8+10)²=√36+36+324=√396=6√11
AC=√(-2-1)²+(6-2)²+(8+4)²=√9+16+144=√169=13
cosA=(AB²+AC²-BC²)/2AB*AC=(49+169-396)/2*7*13=-178/182=-89/91
cosB=(AB²+BC²-AC²)/2AB*BC=(49+396-169)/2*7*6√11=276/84√11=23/7√11
cosC=(AC²+BC²-AB²)/2AC*BC=(169+396-49)/2*13*6√11=516/156√11=43/13√11