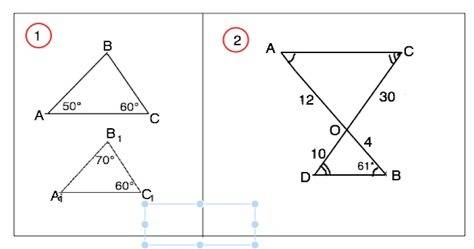
1) Сумма углов треугольника 180°. В ∆ АВС угол В=180°-50°-60°=70°. В ∆ А1В1С1 угол А1=180°-708-608=50°. Треугольники АВС и А1В1С1 подобны по равенству всех углов.
2) По условию АС║BD, АВ и СD - секущие. Образовавшиеся при пересечении секущими параллельных прямых накрестлежащие углы равны. ⇒ ∠СAО=∠DBO=61°. Треугольники АОС и BOD подобны по равенству накрестлежащих углов, а стороны, содержащие вертикальные углы при О - пропорциональны. k=АО:ВО=12:4=3, k=СО:DO=30:10=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(AOC):S(BOD)=k²=3²=9
MBO - треугольник
BH - высота
BO = 5
OH = 4
Найти:
MB - ?
Решение:
Рассмотрим треугольник BHO; в нем BO = 5, OH = 4 ( по условию ); BH = BO² - OH² = 5² - 4² = 25 - 16 = 9² = 3; следовательно, треугольник BHO - египетский (стороны 3,4,5). Найдем длину сторон MB по теореме синусов. Пусть MB = x. Находим x по формуле 2R*sin (sin см. на фото во вложении ∠O). Исходя из того что треугольник BHO - египетский, находим sin =