12 см, 20 см, 28 см
Объяснение:
Если я правильно понял условие, то решение будет таким:
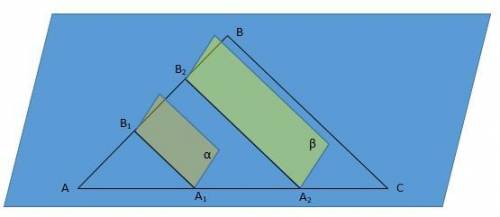
Т.к. треугольник равносторонний, то АВ=ВС=АС=12.
Поскольку АВ₁=В₁В₂=В₂В, то
АВ₁=В₁В₂=В₂В=АВ:3=12:3=4
По теореме Фалеса
АА₁=А₁А₂=А₂С=АС:3=12:3=4
Треугольники АВ₁А₁, АВ₂А₂ и АВС подобные. Значит, треугольники АВ₁А₁ и АВ₂А₂ тоже будут равносторонними. На основании этого
В₁А₁=АВ₁=4
В₂А₂=АВ₂=2АВ₁=8
Данный треугольник АВС разбивается на треугольник АВ₁А₁ и трапеции А₁В₁В₂А₂ и А₂В₂ВС.
Находим их периметры.
Р(АВ₁А₁)=3АВ₁=3*4=12
Р(А₁В₁В₂А₂)=А₁В₁+В₁В₂+А₂В₂+А₁А₂=4+4+8+4=20
Р(А₂В₂ВС)=А₂В₂+В₂В+ВС+А₂С=8+4+12+4=28
х = (- 2 - 2)/2 = - 2
у = (2 + 0) /2 = 1
z = (0 - 4)/2 = - 2
M(-2, 1, -2)
AM = √(-2-1)² + (1 -3)² + ( -2-5)² = √(9 + 4 + 49) = √62