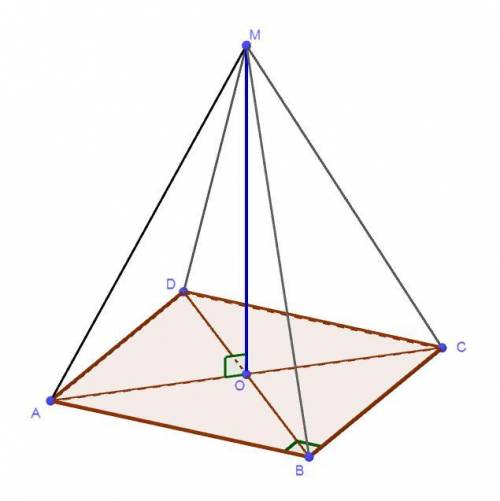
Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.
Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк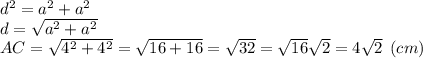
а пересечения делит их пополам.
Р-м ΔAOM:
∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.
AO = d/2
Ищем, чему равна диагональ квадрата:
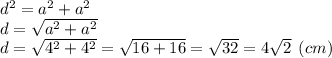
AO = (4√2)/2 = 2√2 см
Теперь можем найти длину отрезка AM
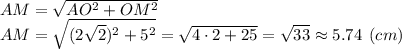
ответ: Расстояние равно √33 см, или приблизительно 5,74 см.
Дано:
ABCD - ромб
диагональ АС = 6√3 см
сторона ромба 6 см
Найти: углы ромба
Решение
Рассмотрим ΔАОВ. Он прямоугольный, так как диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам.
АВ = 6 см - гипотенуза ΔАОВ;
АО = АС:2 = (6√3) :2 = 3√3 см - катет рассматриваемого треугольника АОВ.
найдем второй катет ОВ.
ОВ²=АВ²-АО² = 6²- (3√3)² = 36-27=9
ОВ = √9 = 3 см.
Так как катет ОВ равен половине гипотенузы АВ, то напротив него лежит угол 30°. (∠ОАВ).
Соответственно, ∠АВО = 90-30 = 60°.
Так как диагонали ромба делят углы ромба пополам, несложно посчитать все углы ромба. Противоположные углы ромба равны.
∠DAB = ∠BCD = 30*2 = 60°
∠ADC = ∠ABC = 60*2 = 120°
ответ: углы ромба 60°, 60°, 120°, 120°.
Против большего угла в треугольнике лежит большая сторона и наоборот.
Сторона 13 см - большая в треугольнике, значит против нее лежит больший угол - прямой, т.е. 90⁰