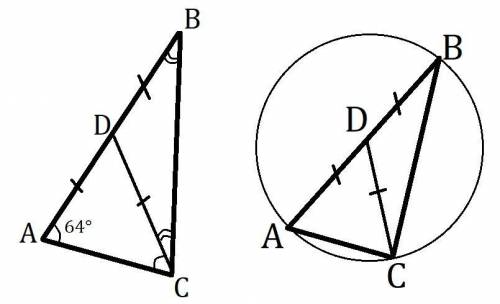
CD - медиана ΔABC, поэтому AD=DB, по условию BD=CD значит, AD=BD=CD
1ыйΔADC - равнобедренный (AD=CD), поэтому ∠ACD=∠CAD=64° и ∠ADC = 180°-2∠CAD = 180°-2·64° = 52°.
∠CDB = 180°-∠ADC = 180°-52° = 128°, как смежный угол.
ΔCDB - равнобедренный (BD=CD), поэтому ∠DCB=∠DBC=(180°-∠CDB)/2 = (180°-128°)/2 = 26°
∠ACB = ∠ACD+∠DCB = 64°+26° = 90°
2ойТочка D равноудалена от вершин ΔABC (AD=DC=DB), поэтому это центр описанной окружности. D∈AB ⇒ AB - диаметр.
Вписанный угол опирающийся на диаметр равен 90°.
∠ACB - вписанный и опирается на AB значит, ∠ACB=90°
ответ: 90°.
AB/cosx=BM/sinx,
ABtgx=BM,
tgx=BM/AB.
Из треугольника ABH sin2x=BH/AB=9*BM/(5*AB)⇒9/5*tgx=sin2x,
sin2x*5/9=tgx,
10/9*sinx*cosx=sinx/cosx,
10cosx/9=1/cosx,
cosx=+-3√10/10, 0<x<π/2⇒cosx=3√10/10⇒sinx=√10/10⇒sin2x=3/5.
По теореме синусов (рассматриваем треугольник ABC) BC/sin2x=2R,
R=BC/2sin2x=6/(2*3/5)=5
ответ: 5.