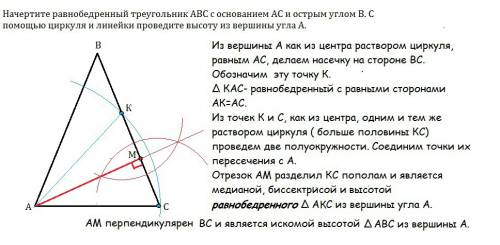
Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Объяснение:
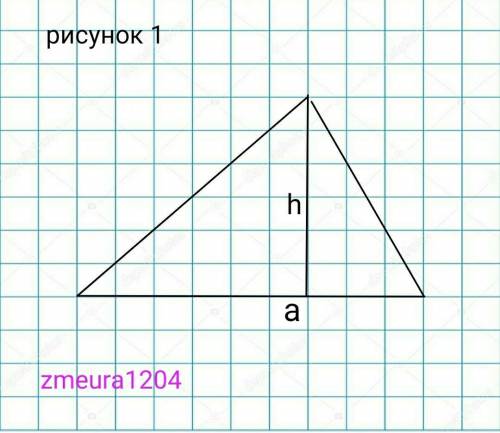
1) рисунок 1.
Дано:
Треугольник
а=48см
S=72cм²
h=?
Решение
S=1/2*a*h, где а- сторона треугольника, h- высота опущенная на сторону а.
h=2*S/a=2*72/48=3 см
ответ: 3см.
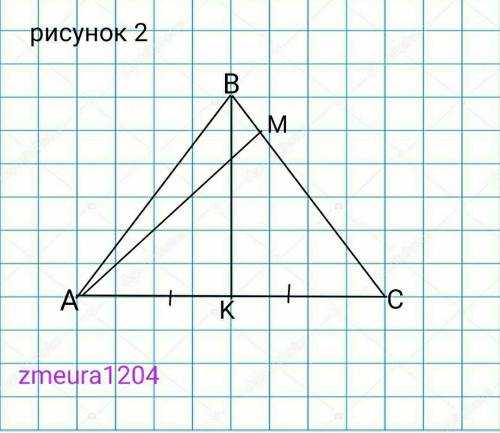
2) рисунок 2
Дано
∆АВС- равнобедренный
АВ=ВС
АС=20см
ВК=24см
АС=?
Решение
ВК- высота, медиана и биссектрисса, равнобедренного треугольника ∆АВС.
АК=КС
КС=АС:2=20:2=10см.
∆ВКС- прямоугольный треугольник.
По теореме Пифагора
ВС=√(ВК²+КС²)=√(24²+10²)=26см.
S=1/2*BK*AC=1/2*24*20=240 см²
S=1/2*AM*BC
AM=2*S/BC=2*240/26=480/26=
=18цел6/13 см
ответ: АМ=18цел6/13 см
Образующая = х, диаметр = 3х
х·3х + 108
3х² = 108
х² = 36
х = 6 ( высота H цилиндра)
диаметр = 18⇒ радиус(R) = 9
S полн. = 2πRH + 2πR² =2π·9·6 + 2π·36 = 108π + 36π = 144π(cм²)