1.Какая фигура называется четырехугольником?
Четырехугольником называется фигура, которая состоит из четырех точек ( вершин), и четырех последовательно соединяющих их отрезков (сторон), причем никакие три из вершин не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
2.Какие вершины четырехугольника называются соседними, какие –противолежащими?
Соседними называются вершины четырехугольника, которые являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими.
3.Что такое диагональ четырехугольника?
Диагоналями четырехугольника называются отрезки. которые соединяют его противоположные вершины.
4.Как обозначается четырехугольник?
Четырехугольник обычно обозначается латинскими буквами, которые присваиваются каждой вершине.
5.Что такое параллелограмм?
Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
У параллелограмма противолежащие стороны равны и противолежащие углы равны а его диагонали точкой пересечения делятся пополам.
1.Какая фигура называется четырехугольником?
Четырехугольником называется фигура, которая состоит из четырех точек ( вершин), и четырех последовательно соединяющих их отрезков (сторон), причем никакие три из вершин не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
2.Какие вершины четырехугольника называются соседними, какие –противолежащими?
Соседними называются вершины четырехугольника, которые являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими.
3.Что такое диагональ четырехугольника?
Диагоналями четырехугольника называются отрезки. которые соединяют его противоположные вершины.
4.Как обозначается четырехугольник?
Четырехугольник обычно обозначается латинскими буквами, которые присваиваются каждой вершине.
5.Что такое параллелограмм?
Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
У параллелограмма противолежащие стороны равны и противолежащие углы равны а его диагонали точкой пересечения делятся пополам.
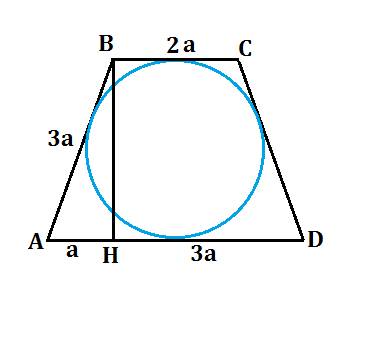
Надо найти величину a.
Известно, r=1. Соединим центр окружности O с точкой касания окружности на стороне AB, Точку касания обозначим P. Отрезок OP- радиус окружности и он перпендикулярен стороне AB. Продлим стороны AB, CD до пересечения. Точку пересечения назовем буквой K. Треугольник AKD-равнобедренный. BC-средняя линия треугольника, так как AD=2BC,BC//AD, как основания трапеции.. Из вершины K треугольника AKD опустим высоту KL, L- точка пересечения с основанием AD, T- точка пересечения с основанием BC. Рассмотрим два треугольника: AKL и OPK. Эти треугольники- подобные. Стороны взаимно перпендикулярны и общий угол. KL перпендикулярна AD, OP перпендикулярна AB, угол K- общий. Запишем пропорцию: AL/OP=KL/PK, AL=a, OP=1, KL= 4 (BC-средняя линия треугольника, LT- высота трапеции, LT=2, точка T лежит на средней линии треугольника, значит высота KL=4), вычислим PK. Рассмотрим треугольник OPK. OP=1 , OK=3.
PK²= OK²-OP², PK²= 3²-1²=9-1=8, PK=√8=2√2.
Подставим все величины в пропорцию.
a/1=4/2√2, a= 1·4/2√2, a= 2/√2=2·√2/√2·√2=√2, a =√2,
MN= 1,5a=1,5·√2= 3√2/2.
MN=3√2/2.