Поскольку АВСД параллелограмм угол СДМ=180-уголВСД. В треугольнике МСД уголСМД=180-уголМСД-уголСДМ=180-уголВСД/2-(180-уголВСД)=уголВСД/2. Значит уголСМД=уголМСД=уголВСД/2. Отсюда треугольник МСД равнобедренный и СД=МД=АВ=3. Аналогично доказываем что треугольник АВК также равнобедренный и АВ=АК=3. Отсюда МК=АД-АК-МД=10-3-3=4. Высота Н у параллелограмма АВСД и трапеции ВСМК общая. Отсюда площадь параллелограмма Sавсд=АД*Н=10*Н. Площадь трапеции Sвсмк=(МК+ВС)/2*Н=(4+10)/2*Н=7*Н. Отсюда искомое отношение площадей 7/10. Кстати оно сохраняется при любых значениях острых углов В и Д.
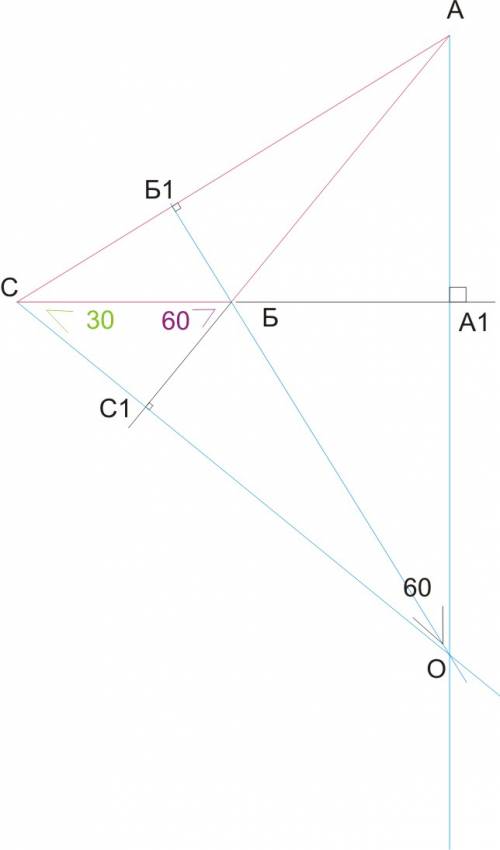
∢Δ СА₁О - прямоугольный, т.к. АА₁-высота к стороне СБ
< А₁ОС=60°, <СА₁О=90° ⇒ <А₁СО=180-(90+60)=30°
∢Δ СС₁Б - прямоугольный, т.к. СС₁ - высота к стороне АБ
<БСС₁=<А₁СО=30°, <СС₁Б=90° ⇒ <СБС₁=180-(90+30)=60°
<АБС =180°-<СБС₁ = 180-60=120°
ответ: <АБС = 120°
или через подобие тр-ков
∢Δ СА₁О подобен ∢Δ СС₁Б по 2-м углам
<СА₁О= <СС₁Б =90°, <БСС₁=<А₁СО - общий = 30° ⇒ <СБС₁=<А₁ОС=60°
<АБС =180°-<СБС₁ = 180-60=120°
ответ: <АБС = 120°
41,03 га=41,03*10 000=410300 м²