Основания трапеции параллельны, каждая боковая сторона при них - секущая. Поэтому сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°, так как они внутренние односторонние.
Обозначим трапецию АВСД. По условию ∠А:∠С=1:2
∠Д:∠В=7:8
Примем угол А=а, тогда угол С=2а.
Примем угол Д=7b, тогда угол В=8b
a+8b=180°
2a+7b=180°
Приравняем левые части уравнений:
а+8b=2a+7b⇒
b=a
Подставим в первое уравнение вместо b - а
Тогда а+8а=180°⇒
а=20°. Следовательно, ∠ВАД=20°, ∠АВС=8•20°=160°;
∠ВСД=2•20=40°; ∠СДА=7•20=140°.
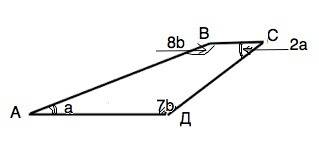
Основания трапеции параллельны, каждая боковая сторона при них - секущая. Поэтому сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°, так как они внутренние односторонние.
Обозначим трапецию АВСД. По условию ∠А:∠С=1:2
∠Д:∠В=7:8
Примем угол А=а, тогда угол С=2а.
Примем угол Д=7b, тогда угол В=8b
a+8b=180°
2a+7b=180°
Приравняем левые части уравнений:
а+8b=2a+7b⇒
b=a
Подставим в первое уравнение вместо b - а
Тогда а+8а=180°⇒
а=20°. Следовательно, ∠ВАД=20°, ∠АВС=8•20°=160°;
∠ВСД=2•20=40°; ∠СДА=7•20=140°.

Обозначим:
ОН = х
ОК = х + 4
В прямоугольнике диагонали точкой пересечения делятся пополам, значит О - середина АС.
ОН║CD как перпендикуляры к одной прямой, ⇒ ОН - средняя линия ΔACD.
CD = 2OH = 2x
ОК - средняя линия треугольника ACD, ⇒ AD = 2OK = 2(x + 4)
Периметр параллелограмма:
2 · (2x + 2(x + 4)) = 56
2x + 2x + 8 = 28
4x = 20
x = 5
CD = 2 · 5 = 10 см
AD = 2 · (5 + 4) = 2 · 9 = 18 см