Объяснение:
Треугольники АOД и ВOС - подобные (уг.ВOС = уг.АOД как вертикальные; уг.СВO = уг.АДO как внутренние накрест лежащие при параллельных прямых АД и ВС и секущей ВД).
Площадь тр-ка ВОС равна S1 = 0,5ВС·Н1
Площадь тр-ка АОД равна S2 = 0,5АД·Н2
При этом Н1:Н2 = к -коэфиициент подобия, а S1 : S2 = к²
S1 : S2 = 0,5ВС·Н1 : 0,5АД·Н2
к² = к· ВС: АД
к = 9/16
Итак, нашли коэффициент подобия.
Из подобия тех же тр-ков следует, что ОВ:ОД = 9/16, но ОД = АС - ОВ и
ОВ: (АС - ОВ) = 9/16
16·ОВ = 9·(АС - ОВ)
16·ОВ = 9·АС - 9·ОВ
25·ОВ = 9·АС
ОВ = 9·АС/25 = 9·18:25 = 6,48
ответ: ОВ = 6,48см
Доброго времени суток!
В условии ошибка : "Острый угол равен 30 см". Углы не измеряются в сантиметрах. Скорее всего, Вы имели ввиду 30°.
▔ ▔ ▔
У равнобедренной трапеции острый угол равен 30°. Вычислите площадь этой трапеции, если длины оснований равны 15 см и 23 см.
▔ ▔ ▔
★☆★ Чертёж смотрите во вложении ★☆★
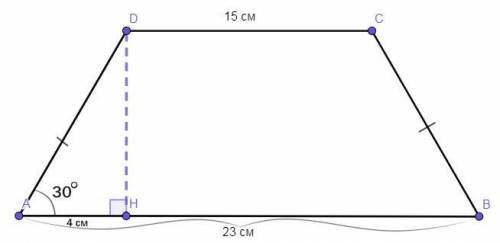
Дано:Четырёхугольник ABCD — равнобедренная трапеция (AD = CB, CD║AB).
∠DAB = 30°.
CD = 15 см.
АВ = 23 см.
Найти:S(ABCD) = ?
Решение:Из вершины ∠ADC на основание АВ опустим высоту DH.
По свойству отрезков, образованных основанием высоты в равнобедренной трапеции, имеем, что —
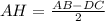
Подставим в формулу известные нам значения —
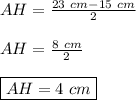
Рассмотрим ΔADH — прямоугольный.
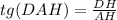
Подставим в формулу известные нам значения —
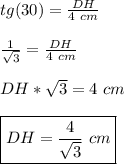
▸Площадь трапеции равна произведению полусуммы оснований и высоты◂
То есть —
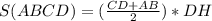
Подставим в формулу известные нам значения —
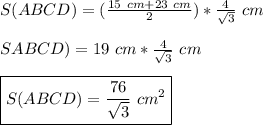
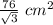

радиус описанной окружности R=2√3
прямая ЕК, параллельная ВС, делит высоту АН в отношении АД/ДН=1/2 (Д - точка пересечения ЕК и АН)
нужно найти ЕК
R=а/√3, откуда сторона а=R√3=2√3*√3=6
высота АН=а√3/2=6√3/2=3√3
АД=АН/3=√3
Т.к. прямая, пересекающая две стороны треугольника, и параллельная третьей, отсекает треугольник, подобный данному, то значит, что ΔАЕК подобен ΔАВС:
АД/АН=ЕК/ВС
ЕК=АД*ВС/АН=√3*6/3√3=2