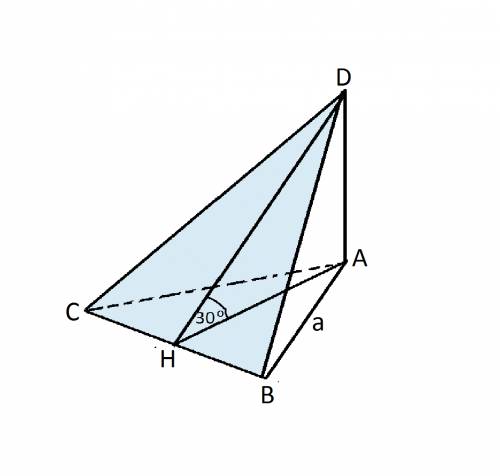
1.Проведём АН -медиану правильного треугольника АВС. Она перпендикулярна стороне ВС, т.к. медиана правильного треугольника одновременно является его высотой.
2.В треугольнике АНС угол Н равен 90 град, сторона АС равна а (по условию), сторона НС равна а/2, т.к. АН-медиана АВС.
АН= sqr(a^2- (a/2)^2)=sqr((3a^2) /4)=(a*sqr3) / 2
3.В треугольнике ДАН угол А равен 90 град, т.к. ДА препенд. пл-ти АВС., угол Н равен 30 град, НА =(a*sqr3) / 2.
Найдём ДА через tg угла ДНС:
tg 30 = ДА / (a*sqr3) / 2, отсюда ДА= а/2
4.Найдём площадь боковой поверхности пирамиды:
S=S(ДАС)+ S(ДАВ)+S(СВД)
S(ДАС)=1/2*АС*АД=1/2*а*а/2=a^2 /4
S(ДАВ)=S(ДАС)=a^2 /4
S(СВД)=1/2*ВС*ДН
ДН найдём из треугольника ДНС ДН= ДА / sin 30= (a/2): 1/2=a
S(СВД)=1/2*a*a=1/2*a^2
S = 2*(a^2 /4) + a^2 /2 = a^2
Дано: ΔABC : AB=BC; BH⊥AC; BO=OH
Найти: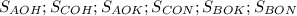
ΔABC - равнобедренный, высота BH является медианой и биссектрисой
⇒ AH = HC ⇒ ΔABH = ΔCBH - по двум катетам. Дальше можно рассматривать только одну половинку равнобедренного треугольника.
У треугольников AOK и BOK одинаковая высота OM. Поэтому их площади будут пропорциональны основаниям AK и KB. Чтобы найти отношение АК:КВ, достроим треугольник ABH до прямоугольника ALBH. LB=AH; AL=BH; LB║AH; AL║BH
∠AKL=∠OKB - вертикальные углы.
∠LAK=∠OBK - накрест лежащие углы при AL║BH и секущей АВ. ⇒
ΔAKL ~ ΔBKO подобны по двум углам:
ответ: площади двух треугольников при основании равны и составляют 1/4 часть площади равнобедренного треугольника;
площади двух треугольников при вершине равны и составляют 1/12 часть площади равнобедренного треугольника;
площади двух треугольников при боковых сторонах равны и составляют 1/6 часть площади равнобедренного треугольника.