Площадь трапеции равна полусумме ее оснований на высоту.
Нам неизвестно ничего =) Будем думать.
В трапецию можно вписать окружность только в том случае, если суммы ее противоположных сторон равны. Так как нам дано, что окружность вписана (ее радиус равен 6), а трапеция равнобедренная, то сумма боковых сторон будет равна 28, и отсюда сумма оснований так же равна 28 (а полусумма 28:2). Радиус вписанной в трапецию окружности равен половине высоты. То есть высота получается равной 12 (2*6).
Ну вот и все. Вычисляйте площадь трапеции на здоровье ;)
14*12
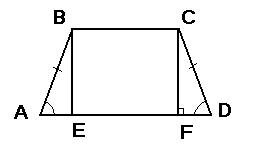
Площадь трапеции = (а+в)*h/2, где а и в - основания трапеции, h-высота. Если опустить из вершины верхнего основания высоту, то получится прямоугольный треугольник АВЕ(на рисунке). Если внимательно его рассмотреть, то мы увидим, что есть прямой угол(90 градусов) и угол при основании равен 45 градусов(угол А), значит угол АВЕ равен 45 градусов(т.к. в треугольнике все три угла в сумме составляют 180 градусов). Отсюда следует, что АЕ=ВЕ, и будут они равны в корень из двух меньше гипотенузы, т.е. 5(т.к. гипотенуза равна 5 корней из двух). ВС=10(меньшее основание) и оно будет равно ЕF. А АЕ=FD(трапеция равнобокая)=5. Значит найдем большее основание = AE+EF+FD=5+10+5=20. ЕВ=h=5. Подставляем в формулу площади S=(10+20)*5/2=150/2=75.
ответ: 75
На рисунке данная призма для большей наглядности «уложена» на плоскость АВВ1А1
Опустим перпендикуляр С1Н из точки С1 наклонной С1В на плоскость АВВ1
С1Н - высота прямоугольного треугольника В1С1А1
Искомый угол -∠С1ВН
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла. ⇒ С1В1²=А1В1*В1Н
5=5*В1Н
В1Н=1
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые она делит гипотенузу.
С1Н²=В1Н*НА1
НА1=В1А1-В1Н=5-1=4
С1Н²=1*4=4
С1Н=√4=2
Sin НВС1=С1Н:ВС1
По т. Пифагора
ВС1=√(ВС²+СС1²)=√(3+5)=√8=2√2
Sin НВС1=2:2√2=1:√2=(√2):2 - это синус 45º