Сделаем рисунок.
Обозначим основание высоты треугольника буквой Н, верхнюю сторону вписанного квадрата КМ, пересечение высоты ВН треугольника со стороной КМ квадрата буквой Е
Стороны квадрата параллельны.
Рассмотрим треугольники АВС и КВМ
Они подобны по равным углам: один общий, другие при параллельных основаниях.
Пусть сторона квадрата КМ=а.
Тогда ВЕ=24-а
Из подобия треугольников справедливо отношение
АВ:КМ=ВН:ВЕ
40:а=24:(24-а)
40*(24-а)=24а
960-40а=24а
960=64а
а= 15 см
Площадь квадрата
S=а²=15²=225 см²
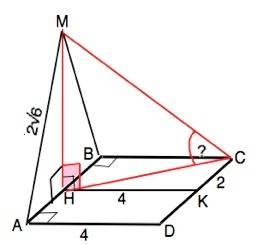
Плоскости квадрата АВСD и треугольника АМВ взаимно перпендикулярны, следовательно, угол МНК между лучами, проведенными из одной точки на их общей стороне АВ перпендикулярно к ней прямой.
МН перпендикулярна плоскости квадрата⇒ перпендикулярна любой прямой, проходящей через её основание Н.
а) ВС и АМ лежат в разных плоскостях, не параллельны и не пересекаются -- они скрещивающиеся.
Чтобы найти угол между скрещивающимися прямыми, нужно провести прямую, параллельную одной из двух скрещивающихся прямых так, чтобы она пересекала вторую прямую. При этом получатся пересекающиеся прямые. Угол между ними равен углу между исходными скрещивающимися.
АМ -наклонная, ее проекция НА перпендикулярна стороне квадрата АD.⇒ АМ⊥АD. Сторона ВС параллельна АD, следовательно, ВС⊥АМ
б) Искомый угол - угол между МС и ее проекцией НС на плоскость квадрата, т.е. угол МСН.
∆ АМВ равнобедренный, его высота МН ещё и медиана ⇒ АН=ВН=2.
По т.Пифагора МН=√(AM²-AH²)=√(24-4)=√20
НС - диагональ прямоугольника НВСК. По т.Пифагора
НС=√(BH²+BC²)=√(4+16)=√20
В прямоугольном ∆ МНС катеты МН=СН ⇒ его острые углы равны 45°
Угол между МС и плоскостью квадрата равен 45°
Известны 2 угла.
Третий угол ( угол В) найдем из суммы углов треугольника:
∠В=180-30°-75°=75°
Т.к. два угла ∆ АВС равны - он равнобедренный, и сторона с=b=4,5
Сторону а найдем по т. синусов.
Теорема синусов:
Стороны треугольника пропорционально синусам противоположных углов:
а: sin∠А = b: sin∠B = c: sin∠C, где a, b, c - стороны треугольника ⇒
а•sin75° =4,5•sin30°
a=4,5•0,5:0,9659
a= ≈2,3294 (единиц длины)