Объяснить пошаговые действия решения .основание прямой призмы abcda1b1c1d1 - ромб abcd с углом a, равным 60 градусов, и стороной, равной 2. найдите высоту призмы, если угол между плоскостями a1bc и abc равен 30 градусов.

👇

Ответ:

Оля142768

03.11.2020

Проведем AE ┴ BC (точка E получается на продолжения СВ:
< ABC =180°- < A =120°) в плоскости ABCD и точка E соединим с точкой A₁,
EC ┴ A₁E (теорема трех перпендикуляров) ⇒<AEA₁ =β=30° будет угол между
плоскостями A₁BC (или A₁BCD₁) и ABC (или ABCD)ю
Из ΔA₁AE: AA₁ =AE*tqα =(AB*sinα)*tqβ =2*sin60°*tq30°=2*( (√3)/2 ) *1/√3 =1.

4,6(77 оценок)

Открыть все ответы

Ответ:

Витуся091

03.11.2020

Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.

Следовательно :

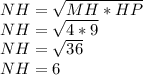
$NH=\sqrt{MH* HP} \\NH=\sqrt{4* 9} \\NH=\sqrt{36}\\NH=6$

Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.

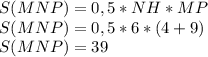
$S(MNP) = 0,5*NH*MP\\S(MNP) = 0,5*6*(4+9)\\S(MNP) = 39\\$

MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.

S(MNPK) = 39*2 = 78.

ответ: 78 (ед^2).

4,4(69 оценок)

Ответ:

hzhwhsbsh

03.11.2020

Постройте рисунок, будет нагляднее.
Пусть трапеция ABCD, BC - меньшее основание, AD - большее, AB - боковая сторона с прямыми углами. Тогда углы ADC и ACB по условию равны и равны 60 градусов.
Средняя линия равна полусумме оснований, т.е. (BC+AD)/2. Надо найти её отношение к BC, а значит выразить AD через BC или наоборот.
Если угол ACB равен 60 градусов, то и угол CAD тоже (не помню верный термин, но потому что AD и BC параллельны). Раз ADC и CAD равны 60, то и ACD равен 60, а значит треугольник ACD - равносторонний. Сторона CD, таким образом, равна AD (и равна AC, но это, как мы увидим, неважно).
Опустим из точки C перпендикуляр к основанию AD, допустим в точку H. Если угол CDH равен 60 градусов, то угол DCH будет 30 градусов. Известно, что против угла в 30 градусов лежит сторона, равная половине гипотенузы. Гипотенуза - CD, и мы узнали что она равна AD. То есть DH = 1/2 CD = 1/2 AD, или, иначе говоря, этот перпендикуляр делит нижнее основание пополам.
В то же время AH = BC, то есть BC = 1/2 AD, или AD = 2 BC
Мы выразили одно основание через другое, подставляем в искомое соотношение:
((BC + AD)/2 ) / BC = (BC + 2 BC) / 2BC = 3/2
Спрашивайте, если что непонятно

4,7(42 оценок)

Это интересно:

Стиль-и-уход-за-собой

28.01.2022

Как окрасить волосы в технике Dip-Dye при помощи Kool Aid?...

Стиль-и-уход-за-собой

02.12.2022

Как создать свой неповторимый образ в стиле 80х...

Компьютеры-и-электроника

11.02.2022

Как установить новые модели машин в GTA 4: подробная инструкция...

Дом-и-сад