Сделаем рисунок.
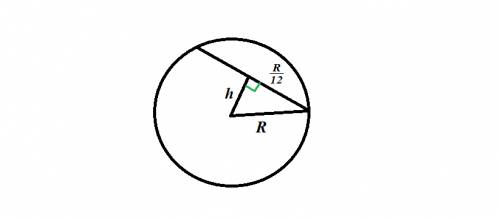
Соединив хонцы хорды с центром окружности,
получим равнобедренный треугольник
с боковыми сторонами, равными радиусу окружности,
и основанием - данной в условии хордой.
Радиус r по условию √2 см
хорда АВ= D:3=2r:3=2√2):3
Проведем из центра окружности к хорде высоту ( медиану) h этого равнобедренного треугольника.
Найдем ее длину по т. Пифагора из прямоугольного треугольника АОМ,
где АО= r,
OM =h ,
AM = AB:2
h²=r²-АМ²
AМ={2√2):3}:2=√2):3
h²=(√2)²- { √2):3}² =2- 2/9
Приведем дробную часть уравнения к общему знаменателю:
h²=(18-2):9=16/9
h=4/3 см
ответ: Расстояние от центра окружности до хорды 4/3 см
Т. к. АВ/А1В1 = 2/3 => k (или коэффициент подобия) = 2/3 =>
АВ = (2*А1В1)/3 (или (2/3)*A1B1)
ВС = (2*В1С1)/3 (или (2/3)*В1С1)
площадь треугольника равна половине произведения двух сторон на синус угла между ними, т. е. Sabc = (1/2) * AB * sinB * BC;
заменяем АВ и ВС через А1В1 и В1С1 соответственно =>
Sabc = (1/2) * (2/3) * А1В1 * sinB * (2/3) * B1C1 = 180
(Sa1b1c1 = (1/2) * A1B1 * sinB * B1C1)
Sa1b1c1 * (4/9) = 180 (через Sa1b1c1 заменяем (1/2)*А1В1*sinB*B1C1, (2/3)*(2/3)=(4/9), а Sabc = 180
Sa1b1c1 = 180 / (4/9) = 405
вроде так
Что и требовалось доказать.