1) Найти высоту трапеции
для решения нужно знать всего ОДНУ формулу
S= (a+b)*h /2 (куда уж проще) где a.b основания трапеции
а) S=175; a=2√3; b=4
175= (4+2√3)*h/2
175*2=(4+2√3)*h
h=350/(4+2√3)= 350*(4-2√3)/ (16-12)= 87.5(4-2√3)
b) S=62; a=3√3; b=6√3
62= (3√3+6√3)*h/2
62*2=(9√3)*h
h= 124/ 9√3= 124√3/18=62√3/9
2) найти тригонометрические функции угла
тут тоже надо знать совсем немного
sin²a+cos²a=1 и sina/ cosa= tga
a) sin d=0.7
cos d = √(1- 0.7²)= √0.51
tg d= sin d/cos d= 0.7/ √0.51
b) tg d=6; sin d= 0.2
cos d= sin d/ tg d= 0.2/ 6 = 0.1/3=1/30
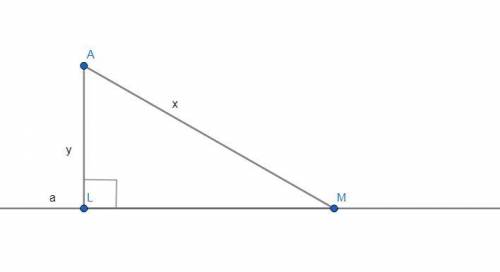
Чертёж смотрите во вложении.
Дано:
а - прямая.
АL - перпендикуляр от точки А до прямой а.
АМ - наклонная от точки А до прямой а.
∠ALM = 90°.
АМ+AL = 11 см.
Разность длин наклонной и перпендикуляра = 1 см.
Найти:
Расстояние от точки А до прямой а = ?
О каком расстоянии идёт речь в задании? Дело в том, что расстояние от точки до прямой - длина перпендикуляра, проведённого из этой точки к этой прямой. Поэтому, мы будем искать длину перпендикуляра AL.Так как АМ - наклонная, то она больше перпендикуляра AL (это не сложно доказать, если рассмотреть получившиеся прямоугольный ΔALM). Итак, поэтому, AM-AL = 1 см.Введём переменные. Пусть АМ = х, а AL = y. Составим систему линейных уравнений и решим её методом подстановки -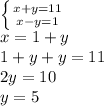
AL = y = 5 см.ответ: 5 см.
