Гипотенуза равна
4+6=10см
По свойству касательных к окружности меньший катет равен меньшему отрезку гипотенузы и неизвестному отрезку касательной у прямого угла
Больший катет равен большему отрезку гипотенузы и неизвестному отрезку касательной у прямоуго угла. Обозначим эти отрезки ( они равны) х.
Составим уравнение нахождения гипотенузы по теореме Пифагора:
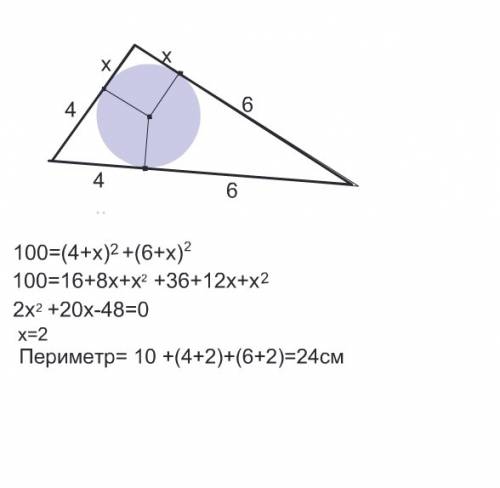
100=(4+х)² +(6+х)²
После преобразований получим квадратное уравнение
2х²+20х-48=0
Решив уравнение чере дискриминант D=784,
получим два корня. Один из них (-12) отрицательный и не подходит.
х=2
Имеем 3 стороны треугольника:
катет 4+2=6 см
катет 6+2=8 см
гипотенузу 10 см
Периметр треугольника равен 24 см
Если из одной точки провести касательные к одной окружности, то отрезки касательных до точек касания будут равны. Поэтому гипотенуза будет 3+10=13/см/, один из катетов 3+х, другой катет равен 10+х.
По теореме ПИфагора (3+х)²+(10+х)²=13²
9+6х+х²+100+20х+х²=169
2х²+26х-60=0; х²+13х-30=0; По теореме, обратной теореме Виета, корни этого уравнения равны х₁=2; х₂=-15 - не подходит по смыслу задачи. Значит, один катет равен 2+3=5/см/, а другой 10+2=12см. Площадь треугольника равна половине произведения катетов, т.е.
5*12/2=30/см²/
SΔABC = 1/2· АС·ВС
Решение.
Опустим перпендикуляр из точки О на АС. Пусть это будет ОК. ΔОКА- прямоугольный, ОК = 1 см, ∠ОАК = 30° ⇒ОА= 2см.
По т. Пифагора АК² = 4 - 1 = 3 ⇒ АК = √3, СК = 1, АС = 1 +√3
АВ = 2(1 + √3). По т . Пифагора ВС² = 4(1 + √3)² - (1 + √3)²= 3(1 + √3)²⇒
,ВС = (1 + √3)·√3
SΔABC = 1/2 ·(1 + √3)·(1 + √3)·√3= √3/2·(1 + 2√3 + 3) =
= √3/2·(4 + √3) = 2√3 + 1, 5