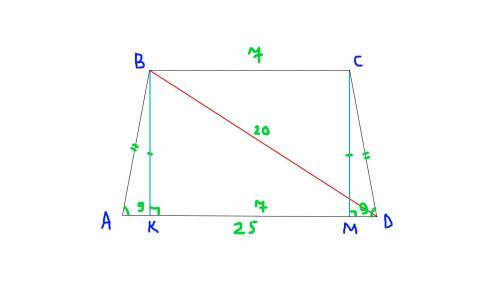
BC = 7
AD = 25
BD = 20
Трапеция равнобедренная
P - ?
----------------------------------------------
1)
Рассмотрим треугольники ABK и DCM (прямоугольные) :
AB = DC (т.к трапеция равнобедренная)
∠BAK = ∠CDM (т.к трапеция равнобедренная)
Значит треугольник ABK = треугольнику DCM => AK = DM
2)
KM = 7
AK = DM = (25 - 7) : 2 = 18 : 2 = 9 (см)
KD = KM + MD = 7 + 9 = 16 (см)
3)
Рассмотри треугольник KBD(прямоугольный) :
По теореме Пифагора :
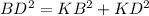
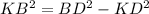
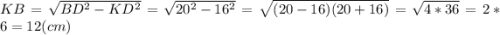
4)
Рассмотри треугольник ABK(прямоугольный) :
По теореме Пифагора :
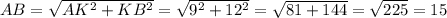 (см)
(см)
5)
P = BC + AD + AB + DC = BC + AD + 2AB = 25 + 7 + 2 * 15 = 32+30 = 62 (см)
ответ : 62 см
Примем боковые стороны , равными а, основание b, медиана m.
Периметры равны: 21 = a + 0,5a + m = 1.5a + m.
12 = m + 0,5a + b.
Вычтем из первого уравнения второе: a - b = 9.
Сторону b заменим: b = a - 9.
Находим длину медианы m = AD для равнобедренного треугольника.
m = (√(2b² + a²))/2 = (√(2(a - 9)² + a²))/2 = (√(2a² - 36a + 162 + a²))/2 =
= (√(3a² - 36a + 162))/2.
Теперь используем полученное значение медианы для периметров треугольников.
21 = 1,5a + (√(3a² - 36a + 162))/2.
(2*21 - 2*1,5a)² = (√(3a² - 36a + 162))².
1764 - 252a + 9a² = 3a² - 36a + 162.
6a² - 216a + 1602 = 0. Сократим на 6.
a² - 36a + 267 = 0.
D=(-36)^2-4*1*267=1296-4*267=1296-1068=228;
Дискриминант больше 0, уравнение имеет 2 корня:
a_1=(√228-(-36))/(2*1)=(√228+36)/2=√57+36/2=√57+18~~25.5498;
a_2=(-√228-(-36))/(2*1)=(-√228+36)/2=-√57+36/2=-√57+18~~10.45017.
Первый корень не принимаем - не соответствует условиям.
ответ: 2 стороны по 18 - √57, третья равна 9 - √57.
один угол равен 100 градусов, другой - 80 ("проверка ответа": 180-20=160; 160:2=80; 80+20=100)
один угол 120, другой - 60 (180:3=60, 180-60=120, 120=60*2)