а где продолжение условия? основанием пирамиды dabc является правильный треугольник abc сторона которого = ребро da перпендикулярно к плоскости авс , а плоскость dbc составляет с плоскостью авс угол 30*. найдите площадь боковой поверхности пирамиды. условие такое? если такое, то вот решение : s(бок) = 2s(адс) + s(всд) угол дка = 30, тогда ад = ак* tg30 = (av3/2)*v3/3 =a/2 тогда s(асд) = 1/2*а*а/2 = а^2 / 4 дк = а, тогда s(всд) = 1/2*а*а = а^2 / 2 s(бок) = 2*(а^2 / 4) * (а^2 / 2) = а^2
ответ: 2 см
Объяснение:
Найдём сначала третью сторону ΔАВС по теореме Пифагора
АС² + ВС² = АВ²
АС² = АВ² - ВС²
АС² = 8² - 4²
АС² = 64 - 16
АС² = 48
АС = √48 = 4√3
Высота прямоугольного треугольника, опущенная из вершины прямого угла вычисляется по формуле: h =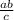 
, где а и в - катеты, с - гипотенуза
h =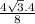 
= 2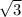
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом: h =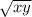 
, где х и у - это отрезки, на которые высота делит гипотенузу.
Пусть BD = х см, тогда АD = (8 - х) см.
Значит, СD =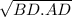 
CD² = BD . AD
(2√3)² = х · ( 8 - х )
х² - 8х + 12= 0
х = 2 или х = 6
Условию задачи удовлетворяет х=2 ( проверяем теорему Пифагора для ΔCBD).
ответ : ВD = 2 см.
Значи
