1)
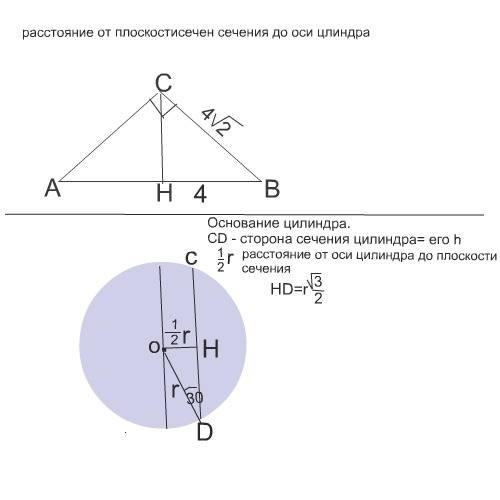
Нарисуем треугольник - осевое сечение конуса. Обозначим его АСВ.
АСВ - равнобедренный прямоугольный треугольник. СВ=d - диагонали квадрата со стороной НВ.
d=а√2
СВ=а√2=4√2, => НВ=4
Площадь полной поверхности конуса равна сумме площади основания и боковой площади.
Sоснов=π r²=π*4²=16π
Sбок= произведению половины длины окружности (2π r):2 на образующую.
Sбок =π r l= π 4*4√2=16√2π
S полная =16π+16√2π=16π(1+√2)
-----------------------------------------------
2)
На рисунке - основание цилиндра.
Треугольник НOD прямоугольный с углом при вершине D=30°, т.к противолежащий катет ОН=половине радиуса r.
НD=ОD*cos(30°)=r(√3):2
CD=cторона сечения=2НD=2r(√3):2=r√3
Площадь сечения - площадь квадрата со стороной CD = 108 см²
CD=√108=6√3
r√3=6√3
r=6
Площадь полной поверхности цилиндра равна сумме площади основания и площади боковой поверхности.
Найдите площадь основания по формуле
S осн=π r²=36π см²
Площадь боковой поверхности цилиндра равна произведению длины окружности на его высоту ( высота равна стороне сечения)
S бок=h* 2 π r=12 π √3
S полн=36π+12 π √3=12π(3+√3)см²
Решение с пояснением:
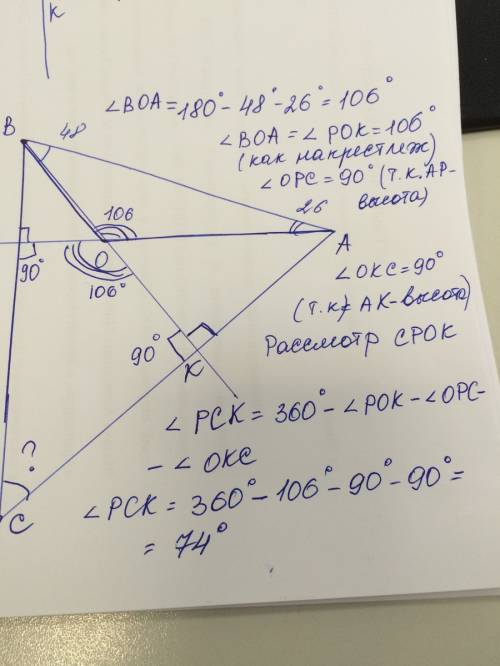
Сума зовнішніх кутів трикутника при кожній вершині = 360 градусів.
З відносини 3: 4: 5 зовнішніх кутів складемо рівняння:
3x+4x+5x=360 градусiв
12 x = 360 градусiв
x = 30 градусiв
кутiв при А = 3x = 3 * 30 = 90 градусiв
кутiв при B = 4x = 4*30 = 120 градусiв
кутiв при С = 5x = 5*30 = 150 градусiв
Зовнішній кут з внутрішньої - суміжні, їх сума дорівнює 180 градусов.Із цього знайдемо всі внутрішні кути:
A = 180 - 90 = 90 градусiв
B = 180 - 120 = 60 градусiв
C = 180 - 150 = 30 градуciв
Трикутник ABC є прямокутним (Кут А дорівнює 90 градусів)
Ознака прямокутного трикутника: навпроти кута в 30 градусів лежить катет, що дорівнює половині від гіпотенузи.
Навпаки кута C лежить катет AB рівний 10 дм т.е BC = AB * 2 = 10 * 2 = 20 дм
Сторона BC трикутника ABC дорівнює 20 дм