Проведем перпендикуляр SO к плоскости основания и перпендикуляры SK, SM и SN к сторонам ΔABC. Тогда по теореме о трех перпендикулярах OK ⊥ BC, ОМ ⊥ АС и ON ⊥ AB.
Тогда, ∠SKO = ∠SMO = ∠SNO = 45° — как линейные углы данных двугранных углов.
А следовательно, прямоугольные треугольники SKO, SMO и SNO равны по катету и острому углу.
Так что OK=OM=ON, то есть точка О является центром окружности, вписанной в ΔАВС.
Выразим площадь прямоугольника АВС:
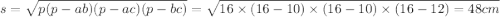
С другой стороны можно S=p×r
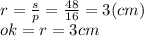
Так как в прямоугольном треугольнике SOK острый угол равен 45°, то ΔSOK является равнобедренным и SO=OK=3 см.
ответ: 3 см.
где AA и BB – некоторые числа. При этом коэффециенты AA и BB одновременно не равны нулю, так как тогда уравнение теряет смысл.
Если C=0C=0, а AA и BB отличны от нуля, то прямая проходит через через начало координат.
Если A=0A=0, а BB и CC отличны от нуля, то прямая параллельна оси OxOx.
Если B=0B=0, а AA и CC отличны от нуля, то прямая параллельна оси OyOy.
Если B=C=0B=C=0, а AA отличен от нуля, то прямая совпадает с осью OyOy.
Если A=C=0A=C=0, а BB отличен от нуля, то прямая совпадает с осью OxOx.
1) Дано: трг АВС-равнобед. угол А=39* , угол В=углу С ( т.к. углы при основании равны).
Зная что сумма всех углов равно 180*
Найти: углы В и С
Решение:
180-39=141-Углы В и С
Углы В и С= 141/2= 70,5
ответ: A=39* B=70,5 C=70,5.
Согласись, ответ не очень красивый.
Дано:трг АВС-равнобед. угол В=39*
Найти: углы С и А
Решение:
угл В=угл С( т.к. углы при основании равны).
39*2=78= Углы В и С
180-78=102-Угл А
ответ: А=102* В=39* С=39*